题目内容
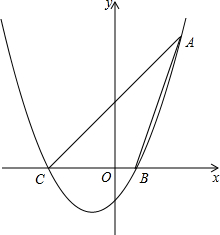 如图,已知二次函数y=
如图,已知二次函数y=| 1 |
| 2 |
(1)求二次函数的解析式及点C的坐标;
(2)若D为线段AC上一点,且以D、O、C为顶点的三角形与△ABC相似,求点D的坐标;
(3)设直线y=1为直线l,将该二次函数的图象在直线l下方的部分沿直线l翻折到直线l上方,图象的其余部分不变,得到一个新图象.是否存在与新图象恰有三个不同公共点且平行于AC的直线?若存在,请求出所有符合条件的直线的解析式;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)将已知点的坐标代入给出的二次函数,利用待定系数法确定两个待定系数的解析式即可;
(2)首先确定线段BC、AC的长,利用△DOC∽△ABC时和△ODC∽△ABC时两种情况根据相似三角形的性质求得有关线段的长,从而求得点D的坐标;
(3)首先确定直线AC的解析式yAC=x+3,设所求直线的解析式为y=x+m.然后设直线l和设l下方的部分翻折后得到的抛物线(部分)为L,将两个解析式联立后得到有关x的方程x2+4x+2m-7=0,再由由△=16-4(2m-7)=0求得m的值即可确定符合条件的直线的解析式.
(2)首先确定线段BC、AC的长,利用△DOC∽△ABC时和△ODC∽△ABC时两种情况根据相似三角形的性质求得有关线段的长,从而求得点D的坐标;
(3)首先确定直线AC的解析式yAC=x+3,设所求直线的解析式为y=x+m.然后设直线l和设l下方的部分翻折后得到的抛物线(部分)为L,将两个解析式联立后得到有关x的方程x2+4x+2m-7=0,再由由△=16-4(2m-7)=0求得m的值即可确定符合条件的直线的解析式.
解答:解:(1)∵二次函数y=
x2+bx+c的图象经过A、B,
∴
,
解得
∴二次函数的解析式为y=
x2+x-
.
令y=0,得x1=1,x2=-3.
∴点C的坐标为(-3,0).
(2)易得BC=4,AC=6
.
①当△DOC∽△ABC时,有
=
,
即
=
,
解得DC=
.
∵过D作DE⊥x轴于E,易得△CDE是等腰直角三角形.
∴CE=DE=
,OE=
,
∴D1(
,
).
②当△ODC∽△ABC时,有
=
,
即
=
,
解得DC=
.
同理可得 D2(-2,1).
综上,点D的坐标为(
,
)或(-2,1).
(3)由已知得yAC=x+3,设所求直线的解析式为y=x+m.
①设直线l:y=1与抛物线的左交点为P,则过P且平行于AC的直线恰与新图象有三个不同的公共点.
令y=1,得
x2+x-
=1,
解得x1=-1+
,x2=-1-
.
∴P(-1-
,1)
把P代入y=x+m,得m=2+
.
∴y=x+2+
②设l下方的部分翻折后得到的抛物线(部分)为L,则与AC平行且与L相切的直线也符合条件.
由题意,易得L的解析式为y=-
(x+1)2+4.
联立
消去y整理得x2+4x+2m-7=0
∵由△=16-4(2m-7)=0,
得m=
.
∴y=x+
.
综上所述,存在两条符合条件的直线,分别是y=x+2+
和y=x+
.
| 1 |
| 2 |
∴
|
解得
|
∴二次函数的解析式为y=
| 1 |
| 2 |
| 3 |
| 2 |
令y=0,得x1=1,x2=-3.

∴点C的坐标为(-3,0).
(2)易得BC=4,AC=6
| 2 |
①当△DOC∽△ABC时,有
| DC |
| AC |
| OC |
| BC |
即
| DC | ||
6
|
| 3 |
| 4 |
解得DC=
| 9 |
| 2 |
| 2 |
∵过D作DE⊥x轴于E,易得△CDE是等腰直角三角形.
∴CE=DE=
| 9 |
| 2 |
| 3 |
| 2 |
∴D1(
| 3 |
| 2 |
| 9 |
| 2 |
②当△ODC∽△ABC时,有
| DC |
| BC |
| OC |
| AC |
即
| DC |
| 4 |
| 3 | ||
6
|
解得DC=
| 2 |
同理可得 D2(-2,1).
综上,点D的坐标为(
| 3 |
| 2 |
| 9 |
| 2 |
(3)由已知得yAC=x+3,设所求直线的解析式为y=x+m.
①设直线l:y=1与抛物线的左交点为P,则过P且平行于AC的直线恰与新图象有三个不同的公共点.
令y=1,得
| 1 |
| 2 |
| 3 |
| 2 |
解得x1=-1+
| 6 |
| 6 |
∴P(-1-
| 6 |
把P代入y=x+m,得m=2+
| 6 |
∴y=x+2+
| 6 |
②设l下方的部分翻折后得到的抛物线(部分)为L,则与AC平行且与L相切的直线也符合条件.
由题意,易得L的解析式为y=-
| 1 |
| 2 |
联立
|
∵由△=16-4(2m-7)=0,
得m=
| 11 |
| 2 |
∴y=x+
| 11 |
| 2 |
综上所述,存在两条符合条件的直线,分别是y=x+2+
| 6 |
| 11 |
| 2 |
点评:本题考查了二次函数的综合知识,题目中涉及到了分类讨论、数形结合及待定系数法等数学方法及数学思想,难度较大.

练习册系列答案
相关题目
 在海洋上有一近似于四边形的岛屿,其平面图如图,小明据此构造出该岛的一个数学模型(如图四边形ABCD)来求岛屿的面积,其中∠A=∠D=90°,AB=BC=15千米,CD=3
在海洋上有一近似于四边形的岛屿,其平面图如图,小明据此构造出该岛的一个数学模型(如图四边形ABCD)来求岛屿的面积,其中∠A=∠D=90°,AB=BC=15千米,CD=3 如图,位于A处的海上救援中心获悉:在其北偏东68°方向的B处有一艘渔船遇险,在原地等待营救.该中心立即把消息告知在其北偏东30°相距20海里的C处救生船,并通知救生船,遇险船在它的正东方向B处,现救生船沿着航线CB前往B处救援,若救生船的速度为20海里/时,请问:救生船到达B处大约需要多长时间?(结果精确到0.1小时:参考数据:sin38°≈0.62,cos38°≈0.79,sin22°≈0.37,cos22°≈0.93,sin37°≈0.60,cos37°≈0.80)
如图,位于A处的海上救援中心获悉:在其北偏东68°方向的B处有一艘渔船遇险,在原地等待营救.该中心立即把消息告知在其北偏东30°相距20海里的C处救生船,并通知救生船,遇险船在它的正东方向B处,现救生船沿着航线CB前往B处救援,若救生船的速度为20海里/时,请问:救生船到达B处大约需要多长时间?(结果精确到0.1小时:参考数据:sin38°≈0.62,cos38°≈0.79,sin22°≈0.37,cos22°≈0.93,sin37°≈0.60,cos37°≈0.80)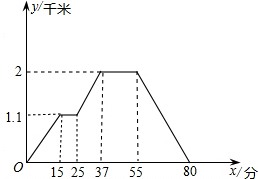 如图的图象反映的过程是:小明从家去菜地浇水,又去玉米地锄草,然后回家,其中x表示时间,y表示小明离他家的距离.根据图象回答下列问题:
如图的图象反映的过程是:小明从家去菜地浇水,又去玉米地锄草,然后回家,其中x表示时间,y表示小明离他家的距离.根据图象回答下列问题:
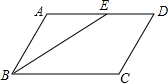 如图,在?ABCD中,BC=9,CD=5,BE平分∠ABC交AD于点E.求DE的长.
如图,在?ABCD中,BC=9,CD=5,BE平分∠ABC交AD于点E.求DE的长. 如图,在△ABC中,∠B=47°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC=
如图,在△ABC中,∠B=47°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC=