��Ŀ����
��ͼ�١��ڣ���ƽ��ֱ������ϵ�У�һ�߳�Ϊ2�ĵȱ�������CDEǡ��������ϵ�еġ�OAB�غϣ��ֽ����ǰ�CDE�Ʊ�AB���е�G��G��Ҳ��DE���е㣩����˳ʱ�뷽����ת180�㵽��C��ED��λ�á�
��1����C�������ꣻ
��2��������O��A��C��������ߵĽ���ʽ��
��3����ͼ�ۣ���G����ABΪֱ����Բ����B������G��������x���ཻ�ڵ�F��������BF�Ľ���ʽ��
��4�����������Ƿ����һ��M��ʹ��S��AMF��S��OAB=16��3�������ڣ��������M�����ꣻ�������ڣ���˵�����ɡ�
��1����C�������ꣻ
��2��������O��A��C��������ߵĽ���ʽ��
��3����ͼ�ۣ���G����ABΪֱ����Բ����B������G��������x���ཻ�ڵ�F��������BF�Ľ���ʽ��
��4�����������Ƿ����һ��M��ʹ��S��AMF��S��OAB=16��3�������ڣ��������M�����ꣻ�������ڣ���˵�����ɡ�

ͼ1 ͼ2 ͼ3
�⣺��1��C�䣨3�� ����
����
��2���������߹�ԭ��O��0��0����
�������߽���ʽΪy=ax2+bx
��A��2��0����C�䣨3�� �����룬��
�����룬��
���a= ��b=-
��b=-
�������߽���ʽΪy= x2-
x2- x��
x��
��3���ߡ�ABF=90�㣬��BAF=60�㣬
���AFB=30��
��AB=2
��AF=4
��OF=2
��F��-2��0��
��ֱ��BF�Ľ���ʽΪy=kx+b
��B��1�� ����F��-2��0�����룬
����F��-2��0�����룬
��
���k= ��b=
��b=
��ֱ��BF�Ľ���ʽΪy= x+
x+ ��
��
��4���ٵ�M��x���Ϸ�ʱ������M��x�� x2-
x2- x��
x��
S��AMF��S��OAB=[ ��4����
��4���� x2-
x2- x��]��[
x��]��[ ��2��4]=16��3
��2��4]=16��3
��x2-2x-8=0��
���x1=4��x2=-2
��x1=4ʱ��y= ��42-
��42- ��4=
��4= ��
��
��x1=-2ʱ��y= ����-2��2-
����-2��2- ����-2��=
����-2��=
��M1��4�� ����M2��-2��
����M2��-2�� ��
��
�ڵ�M��x���·�ʱ�������ڣ����M��x�� x2-
x2- x��
x��
S��AMF��S��OAB=[- ��4����
��4���� x2-
x2- x��]��[
x��]��[ ��2��4]=16��3
��2��4]=16��3
��x2-2x+8=0��b2-4ac��0 ��
�������������ڵ������ΪM1��4�� ����M2��-2��
����M2��-2�� ����
����
 ����
������2���������߹�ԭ��O��0��0����
�������߽���ʽΪy=ax2+bx
��A��2��0����C�䣨3��
 �����룬��
�����룬��
���a=
 ��b=-
��b=-
�������߽���ʽΪy=
 x2-
x2- x��
x����3���ߡ�ABF=90�㣬��BAF=60�㣬
���AFB=30��
��AB=2
��AF=4
��OF=2
��F��-2��0��
��ֱ��BF�Ľ���ʽΪy=kx+b
��B��1��
 ����F��-2��0�����룬
����F��-2��0�����룬��

���k=
 ��b=
��b=
��ֱ��BF�Ľ���ʽΪy=
 x+
x+ ��
����4���ٵ�M��x���Ϸ�ʱ������M��x��
 x2-
x2- x��
x�� S��AMF��S��OAB=[
 ��4����
��4���� x2-
x2- x��]��[
x��]��[ ��2��4]=16��3
��2��4]=16��3��x2-2x-8=0��
���x1=4��x2=-2
��x1=4ʱ��y=
 ��42-
��42- ��4=
��4= ��
����x1=-2ʱ��y=
 ����-2��2-
����-2��2- ����-2��=
����-2��=
��M1��4��
 ����M2��-2��
����M2��-2�� ��
�� �ڵ�M��x���·�ʱ�������ڣ����M��x��
 x2-
x2- x��
x�� S��AMF��S��OAB=[-
 ��4����
��4���� x2-
x2- x��]��[
x��]��[ ��2��4]=16��3
��2��4]=16��3��x2-2x+8=0��b2-4ac��0 ��
�������������ڵ������ΪM1��4��
 ����M2��-2��
����M2��-2�� ����
���� 
��ϰ��ϵ�д�
 �±�Сѧ��Ԫ�Բ���ϵ�д�
�±�Сѧ��Ԫ�Բ���ϵ�д� �ִʾ��ƪϵ�д�
�ִʾ��ƪϵ�д�
�����Ŀ
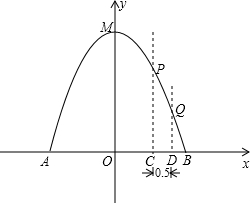 �������Բ����Ͱ�ĺ�Ⱥ��Բ��ƣ�����M��Ϊ���㣬�����߶Գ���Ϊy�ᣬˮƽ����Ϊx�Ὠ��ƽ��ֱ������ϵ��
�������Բ����Ͱ�ĺ�Ⱥ��Բ��ƣ�����M��Ϊ���㣬�����߶Գ���Ϊy�ᣬˮƽ����Ϊx�Ὠ��ƽ��ֱ������ϵ�� ˮ����������ĵ�ˮƽ����Ϊ1m���ﵽ��ߣ��߶�Ϊ3m��
ˮ����������ĵ�ˮƽ����Ϊ1m���ﵽ��ߣ��߶�Ϊ3m��




