Question

【题目】如图，抛物线y=x2﹣2x﹣3与x轴交A、B两点（A点在B点左侧），直线l与抛物线交于A、C两点，其中C点的横坐标为2．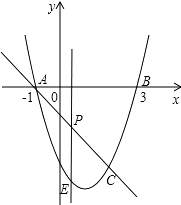

（1）求A、B两点的坐标及直线AC的函数表达式；
（2）P是线段AC上的一个动点，（不与A、C重合），过P点作y轴的平行线交抛物线于E点，求线段PE长度的最大值，并直接写出△ACE面积的最大值；
（3）点G为抛物线上的动点，在x轴上是否存在点F，使A、C、F、G这样的四个点为顶点的四边形是平行四边形？如果存在，直接写出所有满足条件的F点坐标；如果不存在，请说明理由．

Answer 1

【答案】
（1）

解：当y=0时，解得x1=﹣1或x2=3，

∴A（﹣1，0）B（3，0）．

将C点的横坐标x=2代入y=x2﹣2x﹣3得y=﹣3，

∴C（2，﹣3）．

设直线AC的解析式为y=kx+b，将点A和点C的坐标代入得： ，

解得：k=﹣1，b=﹣1．

∴直线AC的函数解析式是y=﹣x﹣1

（2）

解：设P点的横坐标为x（﹣1≤x≤2）则P、E的坐标分别为：P（x，﹣x﹣1），E（x，x2﹣2x﹣3）

∵P点在E点的上方，

∴PE=（﹣x﹣1）﹣（x2﹣2x﹣3）=﹣x2+x+2=﹣（x﹣ ）2+ ．

∴当x= 时，PE的最大值为 ．

∴S△ACE= ×PE×（xC﹣xA）= × ×3=

（3）

解：当AC为平行四边形的对角线时．设点F的坐标为（a，0），点G的坐标为（x，y）．

∵平行四边形的对角线互相平分，

∴依据中点坐标公式可知： ， ．

∴y=﹣3，x=1﹣a．

∵点G在抛物线上，

∴﹣3=（1﹣a）2﹣2（1﹣a）﹣3，整理得：a2﹣1=0，解得a=﹣1或a=﹣1（舍去）．

∴点F的坐标为（1，0）．

当AC为平行四边形的边，CF为对角线时．设点F的坐标为（a，0），点G的坐标为（x，y）．

∵平行四边形的对角线互相平分，

∴依据中点坐标公式可知： ， = ．

∴y=﹣3，x=a+3

∵点G在抛物线上，

∴﹣3=（a+3）2﹣2（a+3）﹣3，整理得：a2+4a+3=0，将a=﹣3或a=﹣1（舍去）

∴点F的坐标为（﹣3，0）．

当AC为平行四边形的边，CG为对角线时．设点F的坐标为（a，0），点G的坐标为（x，y）．

∵平行四边形的对角线互相平分，

∴依据中点坐标公式可知： ， = ．

∴y=3，x=a﹣3

∵点G在抛物线上，

∴3=（a﹣3）2﹣2（a﹣3）﹣3，整理得：a2﹣8a+9=0，解得a=4+ 或a=4 ．

∴点F的坐标为（4+ ，0）或（4﹣ ）．

综上所述，点F的坐标为（1，0）或（﹣3，0）或（4+ ，0）或（4﹣ ）

【解析】（1）令y=0得到关于x的方程，解方程可求得点A和点B的横坐标，将x=2代入抛物线的解析式求得对应的y值可求得点C的纵坐标，设直线AC的解析式为y=kx+b，将点A和点C的坐标代入求得k和b的值即可；（2）设P点的横坐标为x（﹣1≤x≤2）则P、E的坐标分别为：P（x，﹣x﹣1），E（x，x2﹣2x﹣3），然后得到PE与x的函数关系式，利用二次函数的性质可求得PE的最大值，最后依据S△ACE= ×PE×（xC﹣xA）求解即可；（3）设点F的坐标为（a，0），点G的坐标为（x，y），依据中点坐标公式求得点G的坐标，然后将点G的坐标代入抛物线的解析式求得对应的a的值即可．
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识，掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点，以及对二次函数的性质的理解，了解增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．