Question

【题目】如图，半径为2的正六边形ABCDEF的中心在坐标原点O，点P从点B出发，沿正六边形的边按顺时针方向以每秒2个单位长度的速度运动，则第2017秒时，点P的坐标是（ ）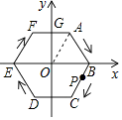
A.（1， ）
B.（﹣1，﹣ ）
C.（1，﹣ ）
D.（﹣1， ）

Answer 1

【答案】C
【解析】解：∵2017=6×336+1， ∴第2017秒时，点P运动到点C，
作CH⊥x轴于H，如图，
∵六边形ABCDEF是半径为1的正六边形，
∴OB=BC=2，∠BCD=120°，
∴∠BCH=30°，
在Rt△BCH中，BH= BC=1，CH= BH= ，
∴OH=OB﹣BH=1，
∴C点坐标为（1，﹣ ），
∴第2017秒时，点P的坐标是（1，﹣ ）．
故选C．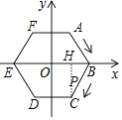

【考点精析】利用数与式的规律对题目进行判断即可得到答案，需要熟知先从图形上寻找规律，然后验证规律，应用规律，即数形结合寻找规律．