题目内容
1.已知一次函数y=kx+b图象上两点A(x1,y1)、B(x2,y2),若x1<x2,则有y1>y2,由此判断下列不等式恒成立的是( )| A. | k>0 | B. | k<0 | C. | b>0 | D. | b≤0 |
分析 由x1<x2时,有y1>y2,得出y随x的增大而减小,根据一次函数的增减性得出k<0.
解答 解:∵一次函数y=kx+b图象上两点A(x1,y1)、B(x2,y2),若x1<x2,则有y1>y2,
∴函数为减函数,图象过第二、四象限,
∴k<0,与b的值没有关系.
故选B.
点评 本题考查了一次函数y=kx+b(k≠0)的图象与性质,当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
12.若代数式$\frac{x+1}{x-3}$有意义,则实数x的取值范围是( )
| A. | x≠-1 | B. | x≥一1且x≠3 | C. | x=3 | D. | x≠3 |
9.下列各式能用平方差公式计算的是( )
| A. | (-2x-1)(1-2x) | B. | (x-3)(3-x) | C. | (x-3)(2x+3) | D. | (-x-3)(x+3) |
16.已知代数式x+2y的值是-2,则代数式3x+6y+1的值是( )
| A. | -3 | B. | -5 | C. | 1 | D. | 3 |
5.计算20102-2007×2013的结果是( )
| A. | 9 | B. | 18 | C. | 2010 | D. | 2013 |
12.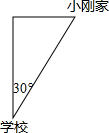 如图所示,小刚家在学校的北偏东30°方向,距离学校2000米,则学校在小刚家的位置是( )
如图所示,小刚家在学校的北偏东30°方向,距离学校2000米,则学校在小刚家的位置是( )
 如图所示,小刚家在学校的北偏东30°方向,距离学校2000米,则学校在小刚家的位置是( )
如图所示,小刚家在学校的北偏东30°方向,距离学校2000米,则学校在小刚家的位置是( )| A. | 北偏东30°,距离小刚家2000米 | B. | 南偏西60°,距离小刚家2000米 | ||
| C. | 南偏西30°,距离小刚家2000米 | D. | 北偏东60°,距离小刚家2000米 |
7.下列说法中,错误的是( )
| A. | -9没有平方根 | B. | 4的算术平方根是2 | ||
| C. | 8的平方根是±2$\sqrt{2}$ | D. | 8的立方根是±2 |
8.下列运算中,正确的是( )
| A. | a2•a3=a6 | B. | a2+a3=a6 | C. | a6÷a2=a4 | D. | 2(a+b)=2a+b |