题目内容
13.已知一直线经过点A(2,$\frac{2}{3}$)和点B(-$\frac{1}{2}$,0).(1)求直线的函数解析式;
(2)画出所求函数的图象.
分析 (1)设直线解析式为y=kx+b,把A与B坐标代入求出k与b的值,即可确定出直线解析式;
(2)在坐标系中描出A与B两点,做出直线即可.
解答 解:(1)设直线解析式为y=kx+b,
把A与B坐标代入得:$\left\{\begin{array}{l}{2k+b=\frac{2}{3}}\\{-\frac{1}{2}k+b=0}\end{array}\right.$,
解得:k=$\frac{4}{15}$,b=$\frac{2}{15}$,
则直线解析式为y=$\frac{4}{15}$x+$\frac{2}{15}$;
(2)做出直线图象,如图所示: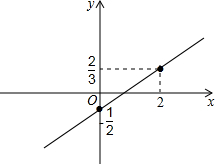
点评 此题考查了待定系数法求一次函数解析式,以及一次函数的图象,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
1.若$\sqrt{{a}^{2}}$=-a,则正确的是( )
| A. | a>0 | B. | a≥0 | C. | a<0 | D. | a≤0 |
5.已知x=6是方程2x-m-4=0的一个解,则m的值是( )
| A. | 8 | B. | 5 | C. | -5 | D. | -8 |
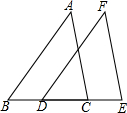 如图,在△ABC和△FDE中,若AB=FD,∠A=∠F,则只需增加条件AC=EF或者增加条件∠B=∠FDE,就可以证明△ABC≌△FDE.(每空只填一个即可)
如图,在△ABC和△FDE中,若AB=FD,∠A=∠F,则只需增加条件AC=EF或者增加条件∠B=∠FDE,就可以证明△ABC≌△FDE.(每空只填一个即可)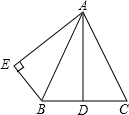 如图,AB=AC,点D是BC的中点,AB平分∠DAE,AE⊥BE,垂足为E.那么AD与AE有什么关系?请说明理由.
如图,AB=AC,点D是BC的中点,AB平分∠DAE,AE⊥BE,垂足为E.那么AD与AE有什么关系?请说明理由.
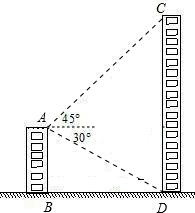 如图,AB和CD是同一地面上的两座楼房,在楼AB的楼顶A点测得楼CD的楼顶C的仰角为45°,楼底D的俯角为30°,已知楼AB的高度为12米.求楼CD的高(结果保留根号).
如图,AB和CD是同一地面上的两座楼房,在楼AB的楼顶A点测得楼CD的楼顶C的仰角为45°,楼底D的俯角为30°,已知楼AB的高度为12米.求楼CD的高(结果保留根号).