题目内容
 如图,∠BAC=110°,AB=AC,若MP和NQ分别垂直平分AB和AC.求∠PAQ的度数.
如图,∠BAC=110°,AB=AC,若MP和NQ分别垂直平分AB和AC.求∠PAQ的度数.分析:求出∠B、∠C度数,根据线段垂直平分线得出BP=AP,CQ=AQ,推出∠BAP=∠B=35°,∠CAQ=∠C=35°即可求出答案.
解答:
解:∵AB=AC,∠BAC=110°
∴∠B=∠C=
(180°-110°)=35°
又∵MP、MQ分别垂直平分AB和AC,
∴BP=AP,CQ=AQ,
∴∠BAP=∠B=35°,∠CAQ=∠C=35°
∴∠PAQ=110°-35°-35°=40°.

解:∵AB=AC,∠BAC=110°
∴∠B=∠C=
| 1 |
| 2 |
又∵MP、MQ分别垂直平分AB和AC,
∴BP=AP,CQ=AQ,
∴∠BAP=∠B=35°,∠CAQ=∠C=35°
∴∠PAQ=110°-35°-35°=40°.
点评:本题考查了等腰三角形的性质,三角形的内角和定理,线段垂直平分线性质的应用,注意:线段垂直平分线上的点到线段两个端点的距离相等.

练习册系列答案
相关题目

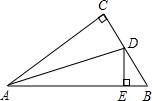 如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,且DE=4.8cm,BC=11.2cm,则BD=
如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,且DE=4.8cm,BC=11.2cm,则BD=
