题目内容
如图所示，∠AOB=90°，∠AOC=40°，∠COD：∠COB=1：2，则∠BOD=
- A.40°
- B.50°
- C.25°
- D.60°
C
分析：先根据∠AOB=90°，∠AOC=40°求出∠COB的度数，再根据∠COD：∠COB=1：2即可得出结论．
解答：∵∠AOB=90°，∠AOC=40°，
∴∠COB=∠AOB-∠AOC=90°-40°=50°，
∵∠COD：∠COB=1：2，
∴∠BOD=
∠BOC=×50°=25°．
故选C．
点评：本题考查的是角的计算，熟知各角度之间的和、差关系是解答此题的关键．
分析：先根据∠AOB=90°，∠AOC=40°求出∠COB的度数，再根据∠COD：∠COB=1：2即可得出结论．
解答：∵∠AOB=90°，∠AOC=40°，
∴∠COB=∠AOB-∠AOC=90°-40°=50°，
∵∠COD：∠COB=1：2，
∴∠BOD=
∠BOC=×50°=25°．故选C．
点评：本题考查的是角的计算，熟知各角度之间的和、差关系是解答此题的关键．
练习册系列答案
芝麻开花课程新体验系列答案
相关题目
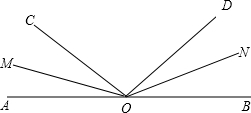如图所示，∠AOB是平角，OM、ON分别是∠AOC、∠BOD的平分线．
74、如图所示，∠AOB=70°，∠COD=80°，求∠AOD-∠BOC的度数．
如图所示，△AOB为正三角形，点A、B的坐标分别为A（2，a），B（b，0），求a，b的值及△AOB的面积．
（2013•邵东县模拟）在平面直角坐标系中，如图所示，△AOB是边长为2的等边三角形，将△AOB绕着点B按顺时针方向旋转得到△DCB，使得点D落在x轴的正半轴上，连接OC，AD．
如图所示，∠AOB=30°，OC平分∠AOB，P为OC上任意一点，PD∥OA交OB于点D，PE⊥OA于点E，若PE=2cm，则PD=