题目内容
18.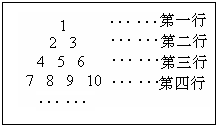 如图所示,是一个自然数排列的三角形数阵:根据该数阵的规律,第6行第3个数是18,第20行第2个数是192.
如图所示,是一个自然数排列的三角形数阵:根据该数阵的规律,第6行第3个数是18,第20行第2个数是192.
分析 观察数据得到第一行有1个数,第二行有2个数,…,即每行的数字的个数等于此行的行数,则第五行最后一个数为1+2+3+4+5=15,再加数三个数得到第6行第3个数;
由于第(n-1)行有(n-1)个数,则第n-1行最后一个数为1+2+3+4+5+…+n-1=$\frac{n(n-1)}{2}$,然后再加两个数即可得到第n行第2个数.
解答 解:第一行有1个数,
第二行有2个数,
第三行有3个数,
第四行有4个数,
第五行有5个数,则第五行最后一个数为1+2+3+4+5=15,
所以第六行有6个数,其中第一个数为16,第二个数为17,第三个数为18,
…
第(n-1)行有(n-1)个数,则第n-1行最后一个数为1+2+3+4+5+…+n-1=$\frac{n(n-1)}{2}$,
所以第n行第一个数为$\frac{n(n-1)}{2}$+1,第二个数为$\frac{n(n-1)}{2}$+2.
当n=20时,$\frac{n(n-1)}{2}$+2=192
故答案为18,192.
点评 本题考查了规律型:数字的变化类:通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.

练习册系列答案
相关题目
9.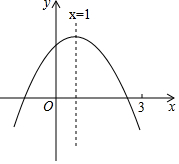 二次函数y=ax2+bx+c(a≠0)图象如图,下列结论正确的是( )
二次函数y=ax2+bx+c(a≠0)图象如图,下列结论正确的是( )
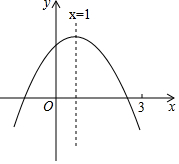 二次函数y=ax2+bx+c(a≠0)图象如图,下列结论正确的是( )
二次函数y=ax2+bx+c(a≠0)图象如图,下列结论正确的是( )| A. | abc>0 | |
| B. | 若ax12+bx1=ax22+bx2且x1≠x2,则x1+x2=1 | |
| C. | a-b+c>0 | |
| D. | 当m≠1时,a+b>am2+bm |
3.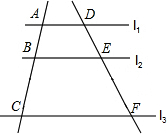 如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于A,B,C和点D,E,F,若$\frac{AB}{BC}$=$\frac{3}{5}$,DE=6,则EF的长是( )
如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于A,B,C和点D,E,F,若$\frac{AB}{BC}$=$\frac{3}{5}$,DE=6,则EF的长是( )
 如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于A,B,C和点D,E,F,若$\frac{AB}{BC}$=$\frac{3}{5}$,DE=6,则EF的长是( )
如图,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于A,B,C和点D,E,F,若$\frac{AB}{BC}$=$\frac{3}{5}$,DE=6,则EF的长是( )| A. | $\frac{18}{5}$ | B. | $\frac{48}{5}$ | C. | 10 | D. | 6 |
10.下列各式中不能用平方差公式进行因式分解的是( )
| A. | 1-a4 | B. | -16a2+b2 | C. | -m4-n4 | D. | 9a2-b4 |
7.一个正方体的截面不可能是( )
| A. | 三角形 | B. | 梯形 | C. | 五边形 | D. | 七边形 |

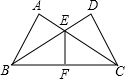 如图,已知∠A=∠D=90°,AB=DC,AC与BD相交于E,F是BC的中点,求证:∠BEF=∠CEF.
如图,已知∠A=∠D=90°,AB=DC,AC与BD相交于E,F是BC的中点,求证:∠BEF=∠CEF.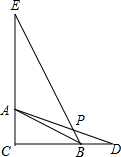 已知,Rt△ABC中∠C=90°,点D在边CB的延长线上,BD=AC,点E在边CA的延长线上,AE=CD,连接BE、AD交于点P,若BC=2BD=2,则PE=$\frac{{9\sqrt{5}}}{5}$.
已知,Rt△ABC中∠C=90°,点D在边CB的延长线上,BD=AC,点E在边CA的延长线上,AE=CD,连接BE、AD交于点P,若BC=2BD=2,则PE=$\frac{{9\sqrt{5}}}{5}$.