题目内容
如图,已知抛物线y=-x2+px+q的对称轴为x=﹣3,过其顶点M的一条直线y=kx+b与该抛物线的另一个交点为N(﹣1,1).要在坐标轴上找一点P,使得△PMN的周长最小,则点P的坐标为( )
| A.(0,2) | B.( ,0) ,0) |
C.(0,2)或( ,0) ,0) | D.以上都不正确 |
A.
解析试题分析:抛物线y=-x2+px+q的对称轴为x=﹣3,可求得p=-6, 抛物线y=-x2+px+q过 点N(﹣1,1),可以求得:q=﹣4,得到抛物线解析式为:y=-x2-6x﹣4,点M(﹣3,5),直线y=kx+b过M,N两点,其解析式为:y=﹣2x+3,作点A使得A与N关于y轴对称,连接MA,与y轴交于点P,易得P(0,2),作点B使得B与N关于x轴对称,连接MB,与x轴交于点Q,易得Q( ),MP<MQ,所以点P的坐标为(0,2).
),MP<MQ,所以点P的坐标为(0,2).
故选A.
考点:1.抛物线解析式,2.轴对称.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
将二次函数 的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是( )
的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是( )
A. | B. |
C. | D. |
对于每个x,函数y是y1=-x+6,y2=-2x2+4x+6这两个函数的较小值,则函数y的最大值是
| A.3 | B.4 | C.5 | D.6 |
抛物线y=x2-2mx+m2+m+1的顶点在( )
| A.直线y=x上 | B.直线y=x-1上 |
| C.直线x+y+1=0上 | D.直线y=x+1上 |
如图所示的二次函数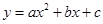 的图象中,刘星同学观察得出了下面四条信息:
的图象中,刘星同学观察得出了下面四条信息:
(1) ;(2)c>1;(3)2a-b<0;(4)a+b+c<0.你认为其中错误的有( )
;(2)c>1;(3)2a-b<0;(4)a+b+c<0.你认为其中错误的有( )
| A.2个 | B.3个 | C.4个 | D.1个 |
把二次函数 的图象向左平移2个单位,再向上平移1个单位,所得到的图象对应的二次函数关系式是( )
的图象向左平移2个单位,再向上平移1个单位,所得到的图象对应的二次函数关系式是( )
A. | B.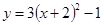 ; ; |
C.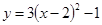 | D.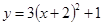 |
当二次函数 取最小值时,
取最小值时, 的值为
的值为
A. | B. | C. | D. |
 的图象如右图所示,则二次函数
的图象如右图所示,则二次函数 的图象大致为
的图象大致为


