题目内容
如图所示的二次函数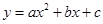
的图象中,刘星同学观察得出了下面四条信息：
（1）
;（2）c>1;（3）2a－b<0;（4）a+b+c<0．你认为其中错误的有（ ）
| A．2个 | B．3个 | C．4个 | D．1个 |
D．
解析试题分析：（1）根据图示知,该函数图象与x轴有两个交点,所以△=b2﹣4ac＞0;故本选项正确;
（2）由图象知,该函数图象与y轴的交点在点（0,1）以下,所以c＜1;故本选项错误;
（3）由图示,知对称轴x=
＞﹣1;又函数图象的开口方向向下,所以a＜0,所以﹣b＜﹣2a,即2a﹣b＜0,故本选项正确;
（4）根据图示可知,当x=1,即y=a+b+c＜0,所以a+b+c＜0;故本选项正确;
综上所述,我认为其中错误的是（2）,共有1个．
故选D．
考点：二次函数图象与系数的关系．
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南大学出版社系列答案
相关题目
如图：点P（x，y）为平面直角坐标系内一点，PB⊥x 轴，垂足为B， A为（0，2），若PA=PB，则以下结论正确的是（ ）．
A．点P在直线 上 | B．点P在抛物线 上 |
C．点P在抛物线 上 | D．点P在抛物线 上 |
下列关于抛物线y=x2+2x+1的说法中,正确的是( )
| A．开口向下 | B．对称轴为直线x=1 |
| C．与x轴有两个交点 | D．顶点坐标为(－1,0) |
如图,已知抛物线y＝－x2＋px＋q的对称轴为x＝﹣3,过其顶点M的一条直线y＝kx＋b与该抛物线的另一个交点为N（﹣1,1）．要在坐标轴上找一点P,使得△PMN的周长最小,则点P的坐标为（ ）
| A．（0,2） | B．（ ,0） |
| C．（0,2）或（,0） | D．以上都不正确 |
抛物线
的对称轴是（ ）
A． | B． | C． | D． |
,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是
，匀减速行驶路程为
，其中
、
为常数. 一汽车经过启动、匀加速行驶、匀速行驶、匀减速行驶之后停车，若把这一过程中汽车的行驶路程
看作时间
的函数，其图象可能是（ ）
把抛物线y=x2向左平移1个单位，所得的新抛物线的函数表达式为（ ）
| A．y=x2+1 | B．y=(x+1) 2 | C．y=x2－1 | D．y=(x－1) 2 |
已知二次函数y＝ax2＋bx＋c（a＜0）的图象如图所示，当－5≤x≤0时，下列说法正确的是（ ）
| A．有最小值－5、最大值0 |
| B．有最小值－3、最大值6 |
| C．有最小值0、最大值6 |
| D．有最小值2、最大值6 |