题目内容
18．
如图，矩形ABCD的对角线AC，BD相交于点O，CE∥BD，DE∥AC．若AC=4，则四边形CODE的周长是8．
分析 先证明四边形CODE是平行四边形，再根据矩形的性质得出OC=OD，然后证明四边形CODE是菱形，即可求出周长．
解答 解：∵CE∥BD，DE∥AC，
∴四边形CODE是平行四边形，
∵四边形ABCD是矩形，
∴OC=$\frac{1}{2}$AC=2，OD=$\frac{1}{2}$BD，AC=BD，
∴OC=OD=2，
∴四边形CODE是菱形，
∴DE=CEOC=OD=2，
∴四边形CODE的周长=2×4=8；
故答案为：8．
点评 本题考查了菱形的判定与性质以及矩形的性质；证明四边形是菱形是解决问题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
请你画出如图几何体的三视图．
6．已知二次函数y=ax2+bx+c的y与x的部分对应值如下表：则下列判断中正确的是（ ）
| x | … | -1 | 0 | 1 | 2 | … |
| y | … | -3 | 1 | 3 | 1 | … |
| A． | 抛物线开口向上 | B． | 抛物线与y轴交于负半轴 | ||
| C． | 当x=3时，y＞0 | D． | 方程ax2+bx+c=0的正根在2与3之间 |
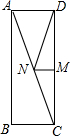如图，在矩形ABCD中，AD=3，AB=9，M是DC上一点，DM=4，N是AC上的一个动点，则△DMN的周长的最小值是$\sqrt{34}$+4．