题目内容
3.解方程:(1)x2-$\sqrt{2}$x-$\frac{1}{4}$=0;
(2)x(x-4)=2-8x;
(3)x2+2$\sqrt{5}$x+10=0.
分析 (1)(3)利用公式法:先找出a,b,c,求出△=b2-4ac的值,再代入求根公式求得答案即可;
(2)化为一般形式,再利用公式法求得方程的解.
解答 解:(1)∵a=1,b=-$\sqrt{2}$,c=-$\frac{1}{4}$,
∴△=b2-4ac=2+1=3,
∴x=$\frac{\sqrt{2}±\sqrt{3}}{2}$.
即x1=$\frac{\sqrt{2}+\sqrt{3}}{2}$,x2=$\frac{\sqrt{2}-\sqrt{3}}{2}$.
(2)x(x-4)=2-8x
整理得x2+4x-2=0,
∵a=1,b=4,c=-2,
∴△=b2-4ac=16+8=24,
∴x=$\frac{-4±2\sqrt{6}}{2}$=.
即x1=-2+$\sqrt{6}$,x2=-2-$\sqrt{6}$
(3)∵a=1,b=2$\sqrt{5}$,c=10,
∴△=b2-4ac=20-40=-20,
∴此方程无解.
点评 本题考查了用公式法解一元二次方程,找出a,b,c,求出△=b2-4ac的值,是解此题的关键.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
 如图,两辆汽车从同一处O出发,分别向东、西方向行驶10km,到达A、B两处,它们的行驶路线相同吗?它们的行驶路程相同吗?
如图,两辆汽车从同一处O出发,分别向东、西方向行驶10km,到达A、B两处,它们的行驶路线相同吗?它们的行驶路程相同吗? 将两个边长为2的小正方形剪拼成一个大正方形(如图),大正方形的边长x是一个无理数,你能估计x的保留两位小数的近似值吗?保留三位小数呢?
将两个边长为2的小正方形剪拼成一个大正方形(如图),大正方形的边长x是一个无理数,你能估计x的保留两位小数的近似值吗?保留三位小数呢?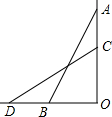 如图,一架25米长的云梯AB斜靠在一面墙上,梯子的底端B距墙角O为7米,若梯子的底部在水平方向滑动了8米到D,则梯子的顶端沿墙下滑了几米?
如图,一架25米长的云梯AB斜靠在一面墙上,梯子的底端B距墙角O为7米,若梯子的底部在水平方向滑动了8米到D,则梯子的顶端沿墙下滑了几米? 如图,OA、OB是⊙O的两条半径,P是$\widehat{AB}$的中点,点C是OA的中点,点D是OB的中点,求证:PC=PD.
如图,OA、OB是⊙O的两条半径,P是$\widehat{AB}$的中点,点C是OA的中点,点D是OB的中点,求证:PC=PD.