题目内容
已知-列数a1、a2、a3、a4、a5、a6、a7,且a1=8,a7=5832, ,则a5为
,则a5为
- A.648
- B.832
- C.1168
- D.1944
A
分析:列数a1、a2、a3、a4、a5、a6、a7,假设
仅知道a1=8,a7=5832,因而要想法用a1,a7表示出k的关系,进而求出k的值.
观察 发现,只有将各式分子分母分别相乘,才能最终剩余a1,a7,k即
发现,只有将各式分子分母分别相乘,才能最终剩余a1,a7,k即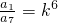
解得k,利用上面的原理也可以化为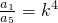 ,那么a5就能解得.
,那么a5就能解得.
解答:令 =k,
=k,
则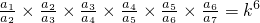 ?
?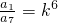 ,
,
即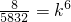 ,
,
解得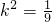 ,
,
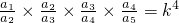 ?
?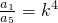 ,
,
解得a5=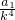 =
=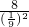 =648.
=648.
故选A.
点评:做好本题的关键是注意观察虚拟一个比值k,再利用已知条件a1=8,a7=5832,k找到他们间的关系,进而找到a1,a5,k间的关系,问题就能解决.本题虽是选择题,但也有一定难度,也可做为大题出现.
分析:列数a1、a2、a3、a4、a5、a6、a7,假设

仅知道a1=8,a7=5832,因而要想法用a1,a7表示出k的关系,进而求出k的值.
观察
 发现,只有将各式分子分母分别相乘,才能最终剩余a1,a7,k即
发现,只有将各式分子分母分别相乘,才能最终剩余a1,a7,k即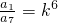
解得k,利用上面的原理也可以化为
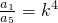 ,那么a5就能解得.
,那么a5就能解得.解答:令
 =k,
=k,则
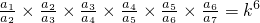 ?
?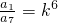 ,
,即
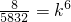 ,
,解得
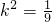 ,
,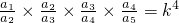 ?
?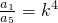 ,
,解得a5=
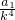 =
=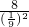 =648.
=648.故选A.
点评:做好本题的关键是注意观察虚拟一个比值k,再利用已知条件a1=8,a7=5832,k找到他们间的关系,进而找到a1,a5,k间的关系,问题就能解决.本题虽是选择题,但也有一定难度,也可做为大题出现.

练习册系列答案
相关题目
 ,请通过计算推算an=________(用含n的代数式表示),a2011=________.
,请通过计算推算an=________(用含n的代数式表示),a2011=________. ,请通过计算推算an= (用含n的代数式表示),a2011= .
,请通过计算推算an= (用含n的代数式表示),a2011= .