题目内容
 已知如图,B、C、E三点在同一条直线上,△ABC和△DCE均为等边三角形,则下列结论:①BD=AE;②△ACF≌△BCM;③MF∥BE;④DMF为等腰三角形.其中正确的结论有
已知如图,B、C、E三点在同一条直线上,△ABC和△DCE均为等边三角形,则下列结论:①BD=AE;②△ACF≌△BCM;③MF∥BE;④DMF为等腰三角形.其中正确的结论有考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:易证△ACE≌△BCD,可得①正确;再证明△ACF≌△BCM,可得②正确;再证明∠CMF=∠ACB,可得③正确,再根据△DMF∽△DBC和BC≠CD≠DM,可得④错误.
解答:解:∵∠ACB=∠DCE=60°,
∴∠DCA=60°,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(SAS),
∴BD=AE,①正确;
∠CBD=∠EAC,
在△ACF和△BCM中,
,
∴△ACF≌△BCM,(ASA),②正确;
∴CM=CN,
∵∠MCN=60°,
∴△CMF是等边三角形,
∴∠CMF=∠ACB=60°,
∴MF∥BE,③正确,
∴△DMF∽△DBC,
∵BC≠CD≠DM,
∴MF≠DF≠DM,④错误;
故答案为 ①②③.
∴∠DCA=60°,
在△ACE和△BCD中,
|
∴△ACE≌△BCD(SAS),
∴BD=AE,①正确;
∠CBD=∠EAC,
在△ACF和△BCM中,
|
∴△ACF≌△BCM,(ASA),②正确;
∴CM=CN,
∵∠MCN=60°,
∴△CMF是等边三角形,
∴∠CMF=∠ACB=60°,
∴MF∥BE,③正确,
∴△DMF∽△DBC,
∵BC≠CD≠DM,
∴MF≠DF≠DM,④错误;
故答案为 ①②③.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ACE≌△BCD和△ACF≌△BCM是解题的关键.

练习册系列答案
相关题目
 作图题:
作图题: 如图,AB是⊙O的直径,点C、D在⊙O上,∠ABC=50°,则∠D的度数为
如图,AB是⊙O的直径,点C、D在⊙O上,∠ABC=50°,则∠D的度数为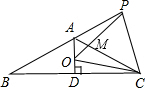 如图,等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP; ④S△ABC=S四边形AOCP,其中正确的有( )
如图,等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP; ④S△ABC=S四边形AOCP,其中正确的有( )