题目内容
关于x的一元二次方程x2－mx＋5(m－5)＝0的两个正实数根
分别为x1、x2，且2x1＋x2＝7，则m的值是( )
A．－2 B．6 C．2或6 D．7
B 解析：由根与系数关系得x1＋x2＝－
＝m，
∵2x1＋x2＝7，∴x1＋m＝7 ∴x1＝7－m，把x1＝7－m代入原方程得
(7－m)2－m(7－m)＋5(m－5)＝0，化简得m2－8m＋12＝0，
解得m1＝2，m2＝6，∵x1·x2＝
＝5(m－5)，当m1＝2时，
x1·x2＝5(m－5)＝－15＜0，与两个正实数根矛盾，舍去，故m＝6.
练习册系列答案
相关题目
C，AD＝3，AB＝5，BC＝9，CD的垂直平分线交BC于E，连结DE，则四边形ABED的周长等于( )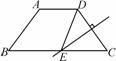
的平均数是5，则另一组
的平均数是（ ）
的自变量x的取值范围是_____________。