题目内容
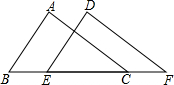 已知:如图,AB=DE,AC=DF,BE=CF.
已知:如图,AB=DE,AC=DF,BE=CF.求证:∠A=∠D.
证明:∵BE=CF
∴BE+
∴BC=
在△ABC和△DEF中,
|
∴
∴∠A=∠D (
考点:全等三角形的判定与性质
专题:推理填空题
分析:易证BC=EF,根据边边边证明三角形全等方法即可求证△ABC≌△DEF即可解题.
解答:解:∵BE=CF (已知),
∴BE+EC=CF+EC(等式性质),
∴BC=EF.(如图)
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS).
∴∠A=∠D (全等三角形对应角相等).
∴BE+EC=CF+EC(等式性质),
∴BC=EF.(如图)
在△ABC和△DEF中,
|
∴△ABC≌△DEF(SSS).
∴∠A=∠D (全等三角形对应角相等).
点评:本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,本题中求证△ABC≌△DEF是解题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
A1,A2,A3,…An(n为正整数)都在数轴上,点A1在原点O的左边,且A1O=1;点A2在点A1的右边,且A2A1=2;点A3在A2的左边,且A3A2=3,点A4在点A3的右边,且A4A3=4…依照上述规律,点A2014,A2015所表示的数分别为( )
| A、2014,-2015 |
| B、-2014,2015 |
| C、1007,-1008 |
| D、1007,-1007 |
 如图所示的几何体甲截面的形状是图乙中的( )
如图所示的几何体甲截面的形状是图乙中的( )A、 |
B、 |
C、 |
D、 |
 如图,点C,E,B,F在同一条直线上,AC∥DF,AC=DF,CE=BF,求证:△ACB≌△DFE.
如图,点C,E,B,F在同一条直线上,AC∥DF,AC=DF,CE=BF,求证:△ACB≌△DFE.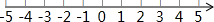 操作:已知在纸面上有一数轴(如图),折叠纸面.
操作:已知在纸面上有一数轴(如图),折叠纸面.
 AB是⊙O的直径,CE⊥AB于E,
AB是⊙O的直径,CE⊥AB于E,