题目内容
 如图,已知线段AB=5cm,点C是以4cm长为半径的⊙A上的一个动点,分别连接BC、AC,若△ABC是直角三角形,则线段BC的长度为
如图,已知线段AB=5cm,点C是以4cm长为半径的⊙A上的一个动点,分别连接BC、AC,若△ABC是直角三角形,则线段BC的长度为3cm或
cm
| 41 |
3cm或
cm
.| 41 |
分析:分两种情况考虑:当∠ACB为直角时,在直角三角形ABC中,由斜边AB及直角边AC的长,利用勾股定理即可求出BC的长;当∠CAB为直角时,由两直角边AC及AB的长,利用勾股定理即可求出斜边BC的长,综上,得到所有满足题意的BC的长.
解答:解:分两种情况考虑:
当∠ACB=90°时,如图所示:

在Rt△ABC中,AB=5cm,AC=4cm,
根据勾股定理得:BC=
=3cm;
当∠CAB=90°时,如图所示:

在Rt△ABC中,AB=5cm,AC=4cm,
根据勾股定理得:BC=
=
cm,
综上,BC的长为3cm或
cm.
故答案为:3cm或
cm
当∠ACB=90°时,如图所示:

在Rt△ABC中,AB=5cm,AC=4cm,
根据勾股定理得:BC=
| AB2-AC2 |
当∠CAB=90°时,如图所示:

在Rt△ABC中,AB=5cm,AC=4cm,
根据勾股定理得:BC=
| AB2+AC2 |
| 41 |
综上,BC的长为3cm或
| 41 |
故答案为:3cm或
| 41 |
点评:此题考查了勾股定理,利用了分类讨论的思想,熟练掌握勾股是解本题的关键.同时本题有两解,注意不要漏解.

练习册系列答案
相关题目
如图,已知线段AB=10cm,点C是AB上任一点,点M、N分别是AC和CB的中点,则MN的长度为( )


| A、6cm | B、5cm | C、4cm | D、3cm |
 如图,已知线段AB,延长AB至C,使得BC=
如图,已知线段AB,延长AB至C,使得BC=| 1 |
| 2 |
| A、4cm | B、8cm |
| C、10cm | D、12cm |


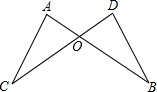 如图,已知线段AB和CD相交于点O,线段OA=OD,OC=OB,求证:△OAC≌△ODB.
如图,已知线段AB和CD相交于点O,线段OA=OD,OC=OB,求证:△OAC≌△ODB.