Question

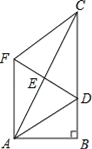
【题目】如图，正方形ABCD的边长为10，点E，F分别为BC，AB边的中点．连接AE、DF，两线交于点H，连接BH并延长，交边AD于点G．下列结论：①△ABE≌△DAF，②cos∠BAE=，③：S四边形CDHE=1：11，④AG=其中正确的是（ ）

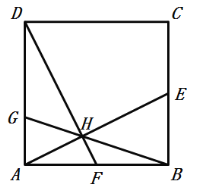
A.①③④B.①②③

C.①④D.②③④

Answer 1

【答案】A

【解析】

利用两对应边成比例且夹角相等可证得①正确；先求得的长，根据角的余弦函数即可说明②错误；分别求得、以及的面积，即可证得③正确；作HQ⊥AB于Q，利用相似三角形的性质求得、、的长，再利用平行线的性质求得的长，④正确；即可判断．

∵正方形ABCD的边长为10，点E，F分别为BC，AB边的中点，

∴，,

∴，∠ABE=∠DAF=90，

∴△ABE≌△DAF，故①正确；

在△ABE中，∠ABE=90，

∴，

∴cos∠BAE=，故②错误；

，

∵△ABE≌△DAF，

∴∠AFH=∠AEB，

∴△AFH△AEB，

∴，

∴，

∴，

∴

，

∴，故③正确；

∵△AFH△AEB，

∴，即，

∴，

作HQ⊥AB于Q，

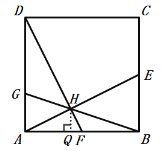
∴HQ∥BE，

∴△AHQ△AEB，

∴，即，

∴，，

∴，

∵HQ∥AG，

∴，即，

∴，故④正确；

综上，①③④正确，

故选：A．