题目内容
14.正方形的边心距为1,则半径为$\sqrt{2}$,边长为2;等边三角形的半径为2,则边长为2$\sqrt{3}$,面积为3$\sqrt{3}$.分析 如图1,据题意首先求出OB、BE的长,即可解决问题.如图2,连接OB,作OD⊥BC于D,则∠ODB=90°,由等边三角形的性质得出∠OBD=30°,BD=$\frac{1}{2}$BC,由三角函数求出OD的数值,再由含30°角的直角三角形的性质得出OB=2OD,即可得出结果.
解答 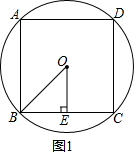 解:如图1,∵四边形ABCD是⊙O的内接正方形,
解:如图1,∵四边形ABCD是⊙O的内接正方形,
∴∠OBE=45°,而OE⊥BC,
∴BE=CE;
∵OE=1,
∴sin45°=$\frac{OE}{BO}$=$\frac{\sqrt{2}}{2}$,
∴OB=$\sqrt{2}$,BC=2,
正方形的边心距为1,则半径为:$\sqrt{2}$,边长为:2;
连接OB,作OD⊥BC于D,如图2所示: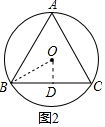
则∠ODB=90°,∠OBD=$\frac{1}{2}$∠ABC=30°,BD=CD=$\frac{1}{2}$BC,
∵OB=2,
∴OD=1,
∴BD=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
BC=2$\sqrt{3}$,
面积=$\frac{1}{2}$×2$\sqrt{3}$×3=3$\sqrt{3}$.
故答案为:$\sqrt{2}$,2,2$\sqrt{3}$,3$\sqrt{3}$.
点评 此题主要考查了圆内接正方形的性质及其应用问题和正三角形的性质和有关计算;解疑的关键是灵活运用有关定理来分析、判断、推理或解答;对综合运用能力提出了一定的要求.

练习册系列答案
相关题目
5.把一张厚度为0.1mm的纸对折8次后厚度接近于( )
| A. | 0.8mm | B. | 2.6cm | C. | 2.6mm | D. | 0.18mm |
 如图所示为立体图形,是由4个面组成的,面与面相交成4条直线,2条曲线.
如图所示为立体图形,是由4个面组成的,面与面相交成4条直线,2条曲线. 如图,五边形ABCDE与五边形A′B′C′D′E′是位似图形,点O是位似中心,位似比为2:1,若五边形ABCDE的面积为16cm2,周长为20cm,那么五边形A′B′C′D′E′的面积为4cm2,周长为10cm.
如图,五边形ABCDE与五边形A′B′C′D′E′是位似图形,点O是位似中心,位似比为2:1,若五边形ABCDE的面积为16cm2,周长为20cm,那么五边形A′B′C′D′E′的面积为4cm2,周长为10cm.