题目内容
 (2013•历下区一模)如图,在矩形ABCD中,AB=
(2013•历下区一模)如图,在矩形ABCD中,AB=| 3 |
分析:连接AC、AC′,则阴影部分的面积为扇形ACA′的面积减去扇形CDD′的面积.
解答:解:连接AC、AC′,

根据勾股定理,得AC=
=2,
故可得S扇形CAA'=
=π,S扇形CDD''=
=
π,
则阴影部分的面积=S扇形CAA'-S扇形CDD''=
π.
故选C.

根据勾股定理,得AC=
| AB2+BC2 |
故可得S扇形CAA'=
| 90π×CA2 |
| 360 |
| 90π×CD2 |
| 360 |
| 3 |
| 4 |
则阴影部分的面积=S扇形CAA'-S扇形CDD''=
| 1 |
| 4 |
故选C.
点评:此题考查了扇形的面积公式和旋转的旋转以及勾股定理,能够把不规则图形的面积转换为规则图形的面积.

练习册系列答案
相关题目
 (2013•历下区一模)如图,设直线l2:y=-2x+8与x轴相交于点N,与直线l1相交于点E(1,a),双曲线y=
(2013•历下区一模)如图,设直线l2:y=-2x+8与x轴相交于点N,与直线l1相交于点E(1,a),双曲线y=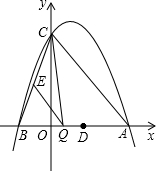 (2013•历下区一模)已知:如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).
(2013•历下区一模)已知:如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).