题目内容
(2013•历下区二模)列方程(组)解应用题:
夏季里某一天,离供电局30千米远的郊区发生供电故障,抢修队接到通知后,立即前去抢修.维修工骑摩托车先走,15分钟后,抢修车装载着所需材料出发,结果两车同时到达抢修点.已知抢修车的速度是摩托车速度的1.5倍,求这两种车的速度.
夏季里某一天,离供电局30千米远的郊区发生供电故障,抢修队接到通知后,立即前去抢修.维修工骑摩托车先走,15分钟后,抢修车装载着所需材料出发,结果两车同时到达抢修点.已知抢修车的速度是摩托车速度的1.5倍,求这两种车的速度.
分析:设摩托车的速度为x千米/时,则抢修车的速度为1.5x千米/时,根据时间之间的等量关系列出方程
=
+
,求出其解就可.
| 30 |
| x |
| 30 |
| 1.5x |
| 15 |
| 60 |
解答:解:设摩托车的速度为x千米/时,则抢修车的速度为1.5x千米/时.根据题意,得
=
+
.
解这个方程,得 x=40.
经检验,x=40是原方程的根.
故抢修车的速度为:1.5x=1.5×40=60.
答:摩托车的速度为40千米/时,抢修车的速度为60千米/时.
| 30 |
| x |
| 30 |
| 1.5x |
| 15 |
| 60 |
解这个方程,得 x=40.
经检验,x=40是原方程的根.
故抢修车的速度为:1.5x=1.5×40=60.
答:摩托车的速度为40千米/时,抢修车的速度为60千米/时.
点评:本题是一道关于行程问题的应用题,考查了分式方程在解决实际问题中的运用.列方程解题的关键是找到等量关系,要注意的是分式方程必须检验.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
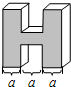 (2013•历下区二模)如图所示的几何体的俯视图是( )
(2013•历下区二模)如图所示的几何体的俯视图是( )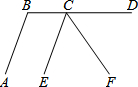 (2013•历下区二模)如图,已知CE∥AB,D为BC延长线上一点,CF平分∠DCE,∠ABD=110°.则∠ECF的度数为( )
(2013•历下区二模)如图,已知CE∥AB,D为BC延长线上一点,CF平分∠DCE,∠ABD=110°.则∠ECF的度数为( )