Question

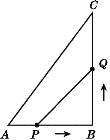
【题目】如图，已知一次函数的图象与坐标轴分别交于A、B点，AE平分，交轴于点E．

（1）直接写出点A和点B的坐标．

（2）求直线AE的表达式．

（3）过点B作BFAE于点F，过点F分别作FD//OA交AB于点D，FC//AB交轴于点C，判断四边形ACFD的形状并说明理由，求四边形ACFD的面积．

Answer 1

【答案】（1）A(0,6)，B(8,0)；（2）y=2x+6；（3）四边形ACFD是菱形，证明见解析；S四边形ACFD=20

【解析】

（1）一次函数，令x=0求出y值，可得A点坐标，令y=0，求出x值，可得B点坐标，此题得解；

（2）已知A，B点坐标，结合勾股定理可求出AB的长度，再利用角平分线的性质即可求出点E的坐标，根据点A、E的坐标利用待定系数法即可求出直线AE的表达式；

（3）过点B作BFAE于点F，过点F分别作FD//OA交AB于点D，FC//AB交轴于点C，连接CD交AF于点G，可得四边形ACFD是平行四边形，证明AD=DF，即可得到四边形ACFD是菱形，证明△AOE∽△BFE，即可得到，，求得BF和EF，进而求得四边形ACFD的面积．

（1）∵

当x=0时，y=6

∴A(0,6)

当y=0时，

解得x=8

∴B(8,0)

∴A(0,6)，B(8,0)

（2）过点E作EM⊥AB于D

∴OA=6，OB=8，

∴AB=

∵AE平分∠BAO，交x轴于点E

∴OE=ME

∴

∴

∴OE=BE

∵OE+BE=OB=8

∴OE=3，BE=5

∴点E的坐标为(3,0)

设直线AE的表达式为y=kx+b

将A(0,6)、E(3,0)代入y=kx+b

解得：

∴直线AE的表达式为y=2x+6

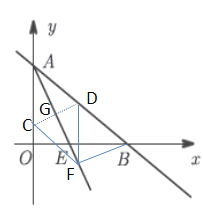
（3）过点B作BFAE于点F，过点F分别作FD//OA交AB于点D，FC//AB交轴于点C，连接CD交AF于点G

∵FD//OA，FC//AB

∴四边形ACFD是平行四边形

∴∠CAF=∠AFD

∵∠CAF=∠FAD

∴∠AFD=∠FAD

∴AD=DF

∴四边形ACFD是菱形

∵∠AOE=∠BFE=90°，∠AEO=∠BEF

∴△AOE∽△BFE

∴

∵OE=3，OA=6

∴AE=

∴

∴BF=

∵四边形ACFD是菱形

∴DG⊥AF，AG=GF

∴DG=BF=

∵

∴

∴EF=

∴AF=AE+EF=

S四边形ACFD=AF×DG=

故答案为：四边形ACFD是菱形，证明见解析；S四边形ACFD=20