题目内容
6.先化简,再求值:($\frac{x+2}{{x}^{2}-2x}$-$\frac{x-1}{{x}^{2}-4x+4}$)÷$\frac{x-4}{x}$,其中x=tan60°+2.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
解答 解:原式=[$\frac{x+2}{x(x-2)}$-$\frac{x-1}{(x-2)^{2}}$]•$\frac{x}{x-4}$=$\frac{{x}^{2}-4-x(x-1)}{x(x-2)^{2}}$•$\frac{x}{x-4}$=$\frac{x-4}{(x-2)^{2}}$•$\frac{1}{x-4}$=$\frac{1}{(x-2)^{2}}$,
当x=tan60°+2=$\sqrt{3}$+2时,原式=$\frac{1}{3}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.-2的倒数是( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -$\frac{1}{2}$ | D. | -2 |
9.下列平面图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
6.若(a-2)2+(b+3)2=0,则(a+b)2015的值是( )
| A. | 0 | B. | 1 | C. | -l | D. | 2012 |
7.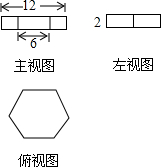 如图所示是某几何体的三视图,则该几何体的体积是( )
如图所示是某几何体的三视图,则该几何体的体积是( )
 如图所示是某几何体的三视图,则该几何体的体积是( )
如图所示是某几何体的三视图,则该几何体的体积是( )| A. | 18$\sqrt{3}$ | B. | 54$\sqrt{3}$ | C. | 108$\sqrt{3}$ | D. | 216$\sqrt{3}$ |
 某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡:
某游泳馆普通票价20元/张,暑假为了促销,新推出两种优惠卡: 如图是一些完全相同的小正方体搭成的几何体的三视图.这个几何体只能是( )
如图是一些完全相同的小正方体搭成的几何体的三视图.这个几何体只能是( )



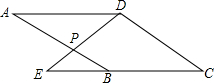 如图,?ABCD中,点P是AB边上的一动点(但不与A,B两点重合),DP的延长线交CB的延长线于点E.
如图,?ABCD中,点P是AB边上的一动点(但不与A,B两点重合),DP的延长线交CB的延长线于点E.