题目内容
如图,直线AB分别交x轴,y轴于A,B,C在y轴上,作∠OCD=∠OAB,CD交OA于D.
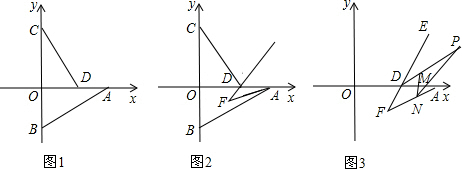
(1)请说明CD和AB位置关系;
(2)∠ADC的平分线DE与∠OAB的平分线交于F,求∠F;
(3)M是线段AD上任意一点(不同于A、D),作MN⊥x轴交AF于N,作∠ADE与∠ANM的平分线交于P点,在前面的条件下,给出下列结论:①∠P-∠MAN的值不变;②∠P的值不变.可以证明,其中有且只有一个结论是正确的,请你作出正确的选择并求值.

(1)请说明CD和AB位置关系;
(2)∠ADC的平分线DE与∠OAB的平分线交于F,求∠F;
(3)M是线段AD上任意一点(不同于A、D),作MN⊥x轴交AF于N,作∠ADE与∠ANM的平分线交于P点,在前面的条件下,给出下列结论:①∠P-∠MAN的值不变;②∠P的值不变.可以证明,其中有且只有一个结论是正确的,请你作出正确的选择并求值.
考点:三角形内角和定理,垂线,三角形的外角性质
专题:
分析:(1)利用等量代换得出∠OCD+∠OBA=90°,说明CD⊥AB即可;
(2)利用角平分线的性质,邻补角的意义以及三角形的内角和定理在△AFD中解决问题即可;
(3)利用角平分线的性质,三角形的内角和,四边形的内角和解决问题即可.
(2)利用角平分线的性质,邻补角的意义以及三角形的内角和定理在△AFD中解决问题即可;
(3)利用角平分线的性质,三角形的内角和,四边形的内角和解决问题即可.
解答:解:(1)CD⊥AB.
如图,
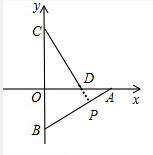
延长CD交AB于点P,
∵∠OBA+∠OAB=90°,∠OCD=∠OAB,
∴∠OBA+∠OCD=90°,
∴∠CPB=180°-(∠OBA+∠OCD)=90°,
∴CD⊥AB.
(2)如图,

∵DE平分∠ADC,AF平分∠OAB,
∴∠ADE=
∠ADC=
(∠COD+∠OCD),∠FAD=
∠BAO,
∴∠FDA=180°-
(∠COD+∠OCD)=135°-
∠OCD,
∵∠OCD=∠OAB,
∴在△ADF中,
∠F=180°-(∠FDA+∠DAF)
=180°-(135°-
∠OCD+
∠BAO)
=180°-135°
=45°.
(3)∠P值不变.
∵∠ADF+∠MNF=360-(∠F+90°)=225°,
∴∠PDA+∠PNM=
(∠EDA+∠ANM)=
(180°-∠ADF+180°-∠MNF)=67.5°,
∠P=360°-∠F-∠ADF-∠MNF-∠PDA-∠PNM=22.5°.
∴∠P值不变.
如图,

延长CD交AB于点P,
∵∠OBA+∠OAB=90°,∠OCD=∠OAB,
∴∠OBA+∠OCD=90°,
∴∠CPB=180°-(∠OBA+∠OCD)=90°,
∴CD⊥AB.
(2)如图,

∵DE平分∠ADC,AF平分∠OAB,
∴∠ADE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠FDA=180°-
| 1 |
| 2 |
| 1 |
| 2 |
∵∠OCD=∠OAB,
∴在△ADF中,
∠F=180°-(∠FDA+∠DAF)
=180°-(135°-
| 1 |
| 2 |
| 1 |
| 2 |
=180°-135°
=45°.
(3)∠P值不变.
∵∠ADF+∠MNF=360-(∠F+90°)=225°,
∴∠PDA+∠PNM=
| 1 |
| 2 |
| 1 |
| 2 |
∠P=360°-∠F-∠ADF-∠MNF-∠PDA-∠PNM=22.5°.
∴∠P值不变.
点评:此题考查三角形的内角和定理,四边形的内角和,角平分线的性质等知识点,注意结合图形,灵活解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
化简
÷(1+
)的结果是( )
| a+1 |
| a2-2a+1 |
| 2 |
| a-1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
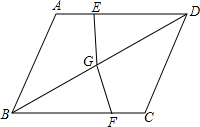 如图,在四边形ABCD中,AD=BC=8,AB=CD,BD=12,点E从点D出发,以每秒1个单位的速度沿DA向点A匀速移动,点F从点C出发,以每秒3个单位的速度,沿C→B→C做匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动,假设移动时间为t秒.
如图,在四边形ABCD中,AD=BC=8,AB=CD,BD=12,点E从点D出发,以每秒1个单位的速度沿DA向点A匀速移动,点F从点C出发,以每秒3个单位的速度,沿C→B→C做匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动,假设移动时间为t秒.