Question

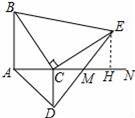
如图所示，线段AB=8cm，射线AN⊥AB于点A，点C是射线上一动点，分别以AC、BC为直角边作等腰直角三角形，得△ACD与△BCE中，连接DE交射线AN于点M，则CM的长为　　　　　　．

　

Answer 1

　4　．

 

【考点】全等三角形的判定与性质；等腰直角三角形．

【分析】如图作EH⊥AN于H，由△ABC≌△HCE得AB=CH，AC=EH，再证明△ABC≌△HCE得CM=CH即可解决问题．

【解答】解：如图作EH⊥AN于H，

∵BA⊥AN，EH⊥AN，

∴∠BAC=∠EHC=90°，

∵∠ABC+∠ACB=90°，∠ACB+∠ECH=90°，

∴∠ABC=∠ECH，

∵△BCE和△ACD都是等腰三角形，

∴BC=CE，AC=DC，∠BCE=∠ACD=90°

在△ABC和△HCE中，

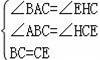
∴△ABC≌△HCE，

∴AC=EH=CD=EH，AB=CH，

在△DCM和△EHM中，

，

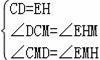
∴△ABC≌△HCE．

∴CM=HM，

∴CM=CH=AB=4．

故答案为4．

【点评】本题考查全等三角形的判定和性质、等腰直角三角形的性质，解题的关键是添加辅助线构造全等三角形，掌握添加辅助线的方法，属于中考常考题型．