题目内容
【题目】在平面直角坐标系![]() 中,
中,![]() 的半径为
的半径为![]() ,点
,点![]() 与圆心
与圆心![]() 不重合,给出如下定义:若在
不重合,给出如下定义:若在![]() 上存在一点
上存在一点![]() ,使
,使![]() ,则称点
,则称点![]() 为
为![]() 的特征点.
的特征点.
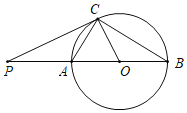
(1)当![]() 的半径为1时,如图1.
的半径为1时,如图1.
①在点![]() ,
,![]() ,
,![]() 中,
中,![]() 的特征点是__________.
的特征点是__________.
②点![]() 在直线
在直线![]() 上,若点
上,若点![]() 为
为![]() 的特征点,求
的特征点,求![]() 的取值范围.
的取值范围.
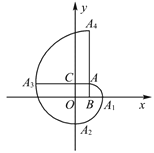
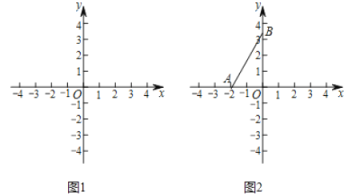
(2)如图2,![]() 的圆心在
的圆心在![]() 轴上,半径为2,点
轴上,半径为2,点![]() ,
,![]() .若线段
.若线段![]() 上的所有点都是
上的所有点都是![]() 的特征点,直接写出圆心
的特征点,直接写出圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
【答案】(1)①![]() ,
,![]() ;②
;②![]() ;(2)
;(2)![]() .
.
【解析】
(1)①根据⊙O的特征点的定义,如果0<OP≤2r(r为⊙O的半径),则点P是⊙O的特征点;
②分两种情形考虑问题:如图1中,当b>0时,设直线y=-![]() x+b与1为半径的⊙O相切于点C,与y轴交于点E,与x轴交于点F.解直角三角形求出OE即可,当b<0时,根据对称性可得结论;
x+b与1为半径的⊙O相切于点C,与y轴交于点E,与x轴交于点F.解直角三角形求出OE即可,当b<0时,根据对称性可得结论;
(2)如图中,取点K(2,0),连接BK.由题意满足条件点C到点B的距离小于等于4且点C到点A的距离小于等于4(点A除外),由此即可解决问题;
(1)①由题意当0<OP≤2r(r为⊙O的半径),则点P是⊙O的特征点,
∵![]() ,
,
![]() =2,
=2,
![]() ,
,
∴![]() ,
,![]() 是特征点,
是特征点,
故答案为:![]() ,
,![]() ;
;
②当![]() 时,设直线
时,设直线![]() 与以1为半径的
与以1为半径的![]() 相切于点
相切于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,
∴![]() ,
,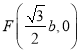 ,
,![]() ,
,
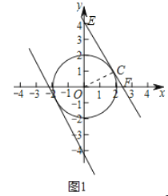
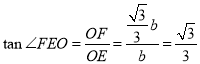 ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
当![]() 时,由对称性可知:
时,由对称性可知:![]() ,
,
∴![]() 的取值范围是
的取值范围是![]() ;
;
(2)如图中,取点K(2,0),连接BK,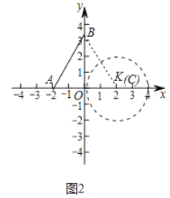
∵点A、B、K的坐标分别为(-2,0),(0,2![]() ),(2,0),
),(2,0),
∴OA=2,OB=2![]() ,OK=2,
,OK=2,
∴AB=![]() ,AK=AO+OK=4,
,AK=AO+OK=4,
![]() ,
,
∴![]() ,
,
∴△ABK是边长为4的等边三角形,
∵线段AB上的所有点都是⊙C的特征点,
∴点C到点B的距离小于等于4且点C到点A的距离小于等于4(点A除外),
∴点C在线段AK上(点A除外),
∴满足条件的m的值为![]() .
.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案【题目】学校运动会的立定跳远和1分钟跳绳两个单项比赛分成预赛和决赛两个阶段.下表为参加这两项比赛的10名学生的预赛成绩:
学生编号 成绩 项目 | 3104 | 3508 | 3115 | 3406 | 3317 | 3413 | 3218 | 3307 | 3519 | 3210 |
立定跳远(单位:米) | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
1分钟跳绳(单位:次) | 163 |
| 175 | 160 | 163 | 172 | 170 |
|
| 165 |
在这10名学生中,同时进入两项决赛的只有6人,进入立定跳远决赛的有8![]() 的值是__________.
的值是__________.
【题目】有这样一个问题:探究函数![]() 的图象和性质.小奥根据学习函数的经验,对函数
的图象和性质.小奥根据学习函数的经验,对函数![]() 的图象和性质进行了探究.下面是小奥的探究过程,请补充完整:
的图象和性质进行了探究.下面是小奥的探究过程,请补充完整:
(1)函数![]() 的自变量
的自变量![]() 的取值范围是_________;
的取值范围是_________;
(2)下表是![]() 与
与![]() 的几组对应值,则
的几组对应值,则![]() 的值为______,
的值为______,![]() 的值为______;
的值为______;
| … |
|
|
|
|
|
|
| 1 | 2 | 3 | 4 | 5 | … |
| … |
|
|
|
|
|
|
|
| 2 |
|
|
| … |
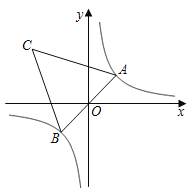
(3)如右图,在平面直角坐标系![]() 中,描出了以上表中各组对应值为坐标的点.根据描出的点,画出该函数的图象;
中,描出了以上表中各组对应值为坐标的点.根据描出的点,画出该函数的图象;
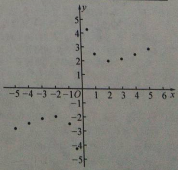
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是![]() .结合函数图象,写出该函数的其他两条性质:①_________,②_________.
.结合函数图象,写出该函数的其他两条性质:①_________,②_________.