题目内容
如图,在梯形 中,
中, ,
, .点
.点 ,
, ,
, 分别在边
分别在边 ,
, ,
, 上,
上, .
.

(1)求证:四边形 是平行四边形;
是平行四边形;
(2)当 时,求证:四边形
时,求证:四边形 是矩形.
是矩形.
【答案】
证明见解析.
【解析】
试题分析:(1)要证明该四边形是平行四边形,只需证明AE∥FG.根据对边对等角∠GFC=∠C,和等腰梯形的性质得到∠B=∠C.则∠B=∠GFC,得到AE∥FG.
(2)在平行四边形的基础上要证明是矩形,只需证明有一个角是直角.根据三角形FGC的内角和是180°,结合∠FGC=2∠EFB和∠GFC=∠C,得到∠BFE+∠GFC=90°.则∠EFG=90°.
试题解析:(1)∵在梯形ABCD中,AB=DC,
∴∠B=∠C.
∵GF=GC,
∴∠C=∠GFC,
∴AB∥GF,即AE∥GF.
∵AE=GF,
∴四边形AEFG是平行四边形;
(2)∵∠FGC+∠GFC+∠C=180°,∠GFC=∠C,∠FGC=2∠EFB,
∴2∠GFC+2∠EFB=180°,
∴∠BFE+∠GFC=90°.
∴∠EFG=90°.
∵四边形AEFG是平行四边形,
∴四边形AEFG是矩形.
考点:1.梯形,2.平行四边形的判定,3.矩形的判定.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在梯形中ABCD中,AD∥BC,∠ABC=90°,BE⊥CD于点E,AB=BE.
如图,在梯形中ABCD中,AD∥BC,∠ABC=90°,BE⊥CD于点E,AB=BE.
 中,
中, ,
, ,
, ,
, ,
, 为
为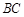 上一动点,则
上一动点,则 周长的最小值为 .
周长的最小值为 .
 中,
中, ∥
∥ ,
, ,
, ,点
,点 在对角线
在对角线 上,作
上,作 ,连接
,连接 ,且满足
,且满足 .
.
 ;
; 时,试判断四边形
时,试判断四边形 的形状,并说明理由.
的形状,并说明理由. 中,
中, 两点在边
两点在边 上,且四边形
上,且四边形 是平行四边形.
是平行四边形.
 与
与 时,求证:平行四边形
时,求证:平行四边形