题目内容
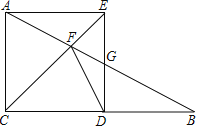
【题目】在Rt△ABC中,∠ACB=90°,AC=12.点D在直线CB上,以CA,CD为边作矩形ACDE,直线AB与直线CE,DE的交点分别为F,G,
(1)如图,点D在线段CB上,四边形ACDE是正方形.
①若点G为DE的中点,求FG的长.
②若DG=GF,求BC的长.
(2)已知BC=9,是否存在点D,使得△DFG是等腰三角形?若存在,求该三角形的腰长;若不存在,试说明理由.
【答案】(1)①![]() ,②12
,②12![]() ;(2)等腰
;(2)等腰![]() 的腰长为4或20或
的腰长为4或20或![]() 或
或![]() .理由见解析.
.理由见解析.
【解析】
(1)①只要证明△ACF∽△GEF,推出![]() ,即可解决问题;②如图1中,想办法证明∠1=∠2=30°即可解决问题;
,即可解决问题;②如图1中,想办法证明∠1=∠2=30°即可解决问题;
(2)分四种情形:①如图2中,当点D在线段BC上时,此时只有GF=GD,②如图3中,当点D在线段BC的延长线上,且直线AB,CE的交点中AE上方时,此时只有GF=DG,
③如图4中,当点D在线段BC的延长线上,且直线AB,EC的交点中BD下方时,此时只有DF=DG,如图5中,当点D中线段CB的延长线上时,此时只有DF=DG,分别求解即可解决问题.
(1)①在正方形![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]() ,
,
②如图1中,
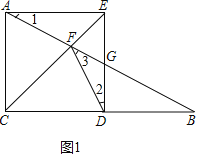
正方形![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,设
,设![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
解得![]() ,
,
![]() ,
,
![]() 在
在![]() 中,
中,![]() .
.
(2)在![]() 中,
中,![]() ,
,
如图2中,
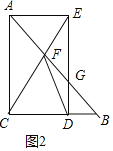
当点![]() 在线段
在线段![]() 上时,此时只有
上时,此时只有![]() ,
,
![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
整理得:![]() ,
,
解得![]() 或5(舍弃)
或5(舍弃)
![]() 腰长
腰长![]() .
.
如图3中,

当点![]() 在线段
在线段![]() 的延长线上,且直线
的延长线上,且直线![]() ,
,![]() 的交点中
的交点中![]() 上方时,此时只有
上方时,此时只有![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
解得![]() 或
或![]() (舍弃),
(舍弃),
![]() 腰长
腰长![]() .
.
如图4中,
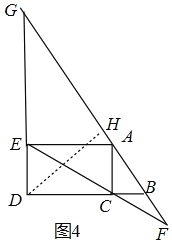
当点![]() 在线段
在线段![]() 的延长线上,且直线
的延长线上,且直线![]() ,
,![]() 的交点中
的交点中![]() 下方时,此时只有
下方时,此时只有![]() ,过点
,过点![]() 作
作![]() .
.
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
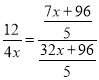 ,
,
解得![]() 或
或![]() (舍弃)
(舍弃)
![]() 腰长
腰长![]() ,
,
如图5中,
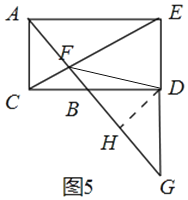
当点![]() 在线段
在线段![]() 的延长线上时,此时只有
的延长线上时,此时只有![]() ,作
,作![]() 于
于![]() .
.
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
 ,
,
解得![]() 或
或![]() (舍弃),
(舍弃),
![]() 腰长
腰长![]() ,
,
综上所述,等腰![]() 的腰长为4或20或
的腰长为4或20或![]() 或
或![]() .
.