题目内容
12.设m是关于x的方程x2-2x+$\frac{1}{4}$(k2-6k+13)=0的一个实数根,求m的值.分析 首先利用配方法得出得出(x-1)2+$\frac{1}{4}$(k-3)2=0,得出k=3,x=1,由此得出m的值即可.
解答 解:∵x2-2x+$\frac{1}{4}$(k2-6k+13)=0,
∴(x-1)2+$\frac{1}{4}$(k-3)2=0,
∴k=3,x=1,
∵m是关于x的方程x2-2x+$\frac{1}{4}$(k2-6k+13)=0的一个实数根,
∴m=1.
点评 此题考查非负数的性质,配方法的运用,一元二次方程根的意义,利用完全平方公式配方是解决问题的关键.

练习册系列答案
相关题目
2.如果正方体的棱长是(a+b)3,那么这个正方体的体积是( )
| A. | (a+b)6 | B. | 6(a+b)6 | C. | (a+b)9 | D. | (a+b)12 |
3.当a>0时,请填表:
| y=ax2 | y=ax2+k | y=a(x-h)2 | y=a(x-h)2+k | |
| 开口方向 | ||||
| 顶点 | ||||
| 对称轴 | ||||
| 最( )值 | ||||
| 增减性 (对称轴右侧) | | | | |
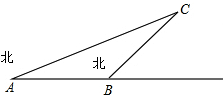 一船在A处测得小岛C在北偏东75°的方向,船在A处向正东航行30海里到B处,再测C在它的东北方向上,求原出发点A与C的距离.
一船在A处测得小岛C在北偏东75°的方向,船在A处向正东航行30海里到B处,再测C在它的东北方向上,求原出发点A与C的距离.