题目内容
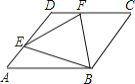
【题目】如图，在边长为1的菱形ABCD中，DAB 60°，E是AD上不同于A，D两点的一动点，F是CD上一点，且AECF1．
（1）证明：无论E，F怎样移动，BEF总是等边三角形；
（2）求BEF 面积的最小值．
【答案】（1）证明见解析；（2）
【解析】
（1）连接
，得到
是等边三角形，由菱形边长为1和
，可得
，利用边角边可以证明
≌
，利用全等三角形的性质推导可得
为等边三角形；
（2）利用的边长表示
，可知当的边长BE最小时就最小，可得当
时BE最小，利用勾股定理求出
，即可求得最小值．
解：（1）如图，连接，
∵四边形ABCD是边长为1的菱形，
∴
，
是等边三角形，
，
，
∴
∵，
，
在和中，
，
，
∴
，
，
∴
，即
，
是等边三角形．
（2）如图，取BE中点为H，连结FH，
∵为等边三角形，
∴FG⊥BE，
设BE=EF=BF=a，则FG=
，
∴
，
∴当的边长最小时，取得最小值，此时BE⊥AD，
∴
，
∴面积的最小值=
．
练习册系列答案
相关题目
