题目内容
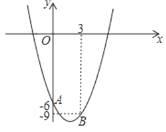
【题目】若关于x的方程x2﹣2ax+a﹣2＝0的一个实数根为x1≥1，另一个实数根x2≤﹣1，则抛物线y＝﹣x2+2ax+2﹣a的顶点到x轴距离的最小值是_____．
【答案】
【解析】
由一元二次方程根的范围结合图形，即可得出关于a的一元一次不等式组，解之即可得出a的取值范围，由二次函数的性质可得出抛物线的顶点坐标，利用配方法即可求出抛物线y=-x2+2ax+2-a的顶点到x轴距离的最小值．
如图，
∵关于x的方程x2-2ax+a-2=0的一个实数根为x1≥1，另一个实数根x2≤-1，
∴
，
解得：-1≤a≤．
抛物线y=-x2+2ax+2-a的顶点坐标为（a，a2-a+2），
∵a2-a+2=（a-
）2+
，
∴当a=
时，a2-a+2取最小值．
故答案为：．
【题目】佳佳向探究一元三次方程x3+2x2﹣x﹣2=0的解的情况，根据以往的学习经验，他想到了方程与函数的关系，一次函数y=kx+b（k≠0）的图象与x轴交点的横坐标即为一元一次方程kx+b（k≠0）的解，二次函数y=ax2+bx+c（a≠0）的图象与x轴交点的横坐标即为一元二次方程ax2+bx+c=0（a≠0）的解，如：二次函数y=x2﹣2x﹣3的图象与x轴的交点为（﹣1，0）和（3，0），交点的横坐标﹣1和3即为x2﹣2x﹣3=0的解．
根据以上方程与函数的关系，如果我们直到函数y=x3+2x2﹣x﹣2的图象与x轴交点的横坐标，即可知方程x3+2x2﹣x﹣2=0的解．
佳佳为了解函数y=x3+2x2﹣x﹣2的图象，通过描点法画出函数的图象．
x | … | ﹣3 | ﹣ | ﹣2 | ﹣ | ﹣1 | ﹣ | 0 |
| 1 |
| 2 | … |
y | … | ﹣8 | ﹣ | 0 |
| m | ﹣ | ﹣2 | ﹣ | 0 |
| 12 | … |
（1）直接写出m的值，并画出函数图象；
（2）根据表格和图象可知，方程的解有 个，分别为 ；
（3）借助函数的图象，直接写出不等式x3+2x2＞x+2的解集．
