题目内容
 已知如图,某小区的中心广场附近有一块四边形空地ABCD,计划改建成个小花圃,经测量,∠C=90°,AB=17m,BC=12m,CD=9m,AD=8m.求:
已知如图,某小区的中心广场附近有一块四边形空地ABCD,计划改建成个小花圃,经测量,∠C=90°,AB=17m,BC=12m,CD=9m,AD=8m.求:(1)对角线BD的长度;
(2)四边形花圃ABCD的面积.
分析:(1)在直角三角形BCD中,根据勾股定理求出BD的长度,
(2)由(1)中BD的长度,再根据勾股定理的逆定理判断出△BCD的形状,再利用三角形的面积公式求解即可.
(2)由(1)中BD的长度,再根据勾股定理的逆定理判断出△BCD的形状,再利用三角形的面积公式求解即可.
解答:解:(1)∵∠C=90°,BC=12m,CD=9m,
∴BD=
=15;
(2)在△ABD中,
∵BD2+AD2=225+64=289=CD2,
∴△ABD是直角三角形,
∴S四边形ABCD=
AD•BD+
BC•CD=
×8×15+
×12×9=114m2.
答:四边形花圃ABCD的面积是114m2.
∴BD=
| BC2 +CD2 |
(2)在△ABD中,
∵BD2+AD2=225+64=289=CD2,
∴△ABD是直角三角形,
∴S四边形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
答:四边形花圃ABCD的面积是114m2.
点评:本题考查的是勾股定理,勾股定理的逆定理及三角形的面积,能根据勾股定理的逆定理判断出△ABD的形状是解答此题的关键.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
 如图,某小区楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡角到楼房的距离CB=8m.在D点处观察点A的仰角为54°,已知坡角为30°,你能求出楼房AB的高度吗?(tan54°≈1.38,结果精确到0.1m)
如图,某小区楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡角到楼房的距离CB=8m.在D点处观察点A的仰角为54°,已知坡角为30°,你能求出楼房AB的高度吗?(tan54°≈1.38,结果精确到0.1m)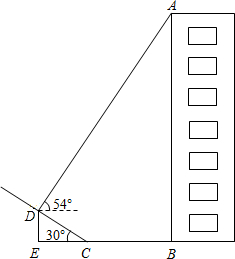 如图,某小区楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡角到楼房的距离CB=8m.在D点处观察点A的仰角为54°,已知坡角为30°,你能求出楼房AB的高度吗?(tan54°≈1.38,结果精确到0.1m)
如图,某小区楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡角到楼房的距离CB=8m.在D点处观察点A的仰角为54°,已知坡角为30°,你能求出楼房AB的高度吗?(tan54°≈1.38,结果精确到0.1m)

