题目内容
如图,某小区楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡角到楼房的距离CB=8m,在D点处观察点A的仰角为54°,已知坡角为30°,你能求出楼房AB的高度吗?(tan54°≈1.38,结果精确到0.1m)

解:过D点作DF⊥AB,交AB于点F,
在Rt△ECD中,CD=6,∠ECD=30°,
∴DE=3=FB,EC=3 ,
,
∴DF=EC+CB=8+3 ,
,
在Rt△ADF中,tan∠ADF= ,
,
∴AF=DF×tan45°,
∴AF=(8+3 )×1.38,
)×1.38,
∴AF≈18.20,
∴AB=AF+FB=18.20+3=21.20≈21.2,
∴楼房AB的高度约是21.2m。
在Rt△ECD中,CD=6,∠ECD=30°,
∴DE=3=FB,EC=3
 ,
,∴DF=EC+CB=8+3
 ,
,在Rt△ADF中,tan∠ADF=
 ,
, ∴AF=DF×tan45°,
∴AF=(8+3
 )×1.38,
)×1.38,∴AF≈18.20,
∴AB=AF+FB=18.20+3=21.20≈21.2,
∴楼房AB的高度约是21.2m。

练习册系列答案
相关题目
 如图,某小区楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡角到楼房的距离CB=8m.在D点处观察点A的仰角为54°,已知坡角为30°,你能求出楼房AB的高度吗?(tan54°≈1.38,结果精确到0.1m)
如图,某小区楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡角到楼房的距离CB=8m.在D点处观察点A的仰角为54°,已知坡角为30°,你能求出楼房AB的高度吗?(tan54°≈1.38,结果精确到0.1m)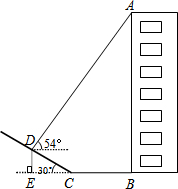 (2012•梧州模拟)如图,某小区楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡脚到楼房的距离CB=8m.在D点处观察楼顶A点的仰角为54°,坡角∠DCE=30°.求楼房AB的高.(结果精确到0.1m)(参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38,
(2012•梧州模拟)如图,某小区楼房附近有一个斜坡,小张发现楼房在水平地面与斜坡处形成的投影中,在斜坡上的影子长CD=6m,坡脚到楼房的距离CB=8m.在D点处观察楼顶A点的仰角为54°,坡角∠DCE=30°.求楼房AB的高.(结果精确到0.1m)(参考数据:sin54°≈0.81,cos54°≈0.59,tan54°≈1.38,
