题目内容
17.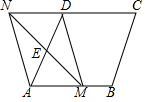 如图,在?ABCD中,点E是AD边的中点,点M在AB边上,DM⊥AB于M,延长ME交射线CD于点N,连接MD,AN.求证:AD=MN.
如图,在?ABCD中,点E是AD边的中点,点M在AB边上,DM⊥AB于M,延长ME交射线CD于点N,连接MD,AN.求证:AD=MN.
分析 由在?ABCD中,点E是AD边的中点,即可证得△DNE≌△AME,则可得DN=AM,又由DN∥AM,即可得四边形AMDN是平行四边形,再结合已知条件DM⊥AB于M,可证明AMDN是矩形,由矩形的性质即可证明AD=MN.
解答 证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
即DN∥AM,
∴∠DNE=∠AME,
∵点E是AD边的中点,
∴DE=AE,
∵在△DNE和△AME中,
$\left\{\begin{array}{l}{∠DNE=∠AME}\\{∠DEN=∠AEM}\\{DE=AE}\end{array}\right.$,
∴△DNE≌△AME(AAS),
∴DN=AM,
∴四边形AMDN是平行四边形,
∵DM⊥AB于M,
∴四边形AMDN是矩形,
∴AD=MN.
点评 本题考查了平行四边形的判定和性质、矩形的判定、以及全等三角形的判定和性质,解题的关键是掌握特殊图形的判定以及重要的性质.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
8.将y=x2向右平移1个单位,再向下平移2单位后,所得表达式是( )
| A. | y=(x-1)2+2 | B. | y=(x+1)2+2 | C. | y=(x-1)2-2 | D. | y=(x+1)2-2 |
7.某自行车厂计划一周生产自行车1400辆,平均每天生产200辆,但由于种种原因,实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产记为正,减产积为负):
(1)根据记录的数据可知该厂本周实际生产自行车多少辆?
(2)该厂实际每日计划计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元,那么该厂工人这一周的工资总额是多少元?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减产值 | +5 | -2 | -4 | +13 | -10 | +16 | -9 |
(2)该厂实际每日计划计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元,那么该厂工人这一周的工资总额是多少元?

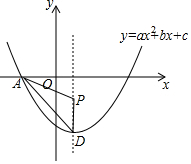 如图,抛物线y=ax2+bx+c的图象与x轴负半轴交于点A(-2,0),顶点D的坐标为(1,-4)
如图,抛物线y=ax2+bx+c的图象与x轴负半轴交于点A(-2,0),顶点D的坐标为(1,-4)