题目内容
8.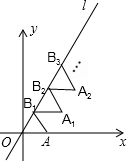 如图,等边三角形△OAB1的一边OA在x轴上,且OA=1,当△OAB1沿直线l滚动,使一边与直线l重合得到△B1A1B2,△B2A2B3,…则点A2017的坐标是($\frac{2019}{2}$,$\frac{2017\sqrt{3}}{2}$).
如图,等边三角形△OAB1的一边OA在x轴上,且OA=1,当△OAB1沿直线l滚动,使一边与直线l重合得到△B1A1B2,△B2A2B3,…则点A2017的坐标是($\frac{2019}{2}$,$\frac{2017\sqrt{3}}{2}$).
分析 根据等边三角形△OAB1的一边OA在x轴上,且OA=1,即可得到A1($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$),再根据A2($\frac{4}{2}$,$\frac{2\sqrt{3}}{2}$),A3($\frac{5}{2}$,$\frac{3\sqrt{3}}{2}$),即可得到规律An($\frac{n+2}{2}$,$\frac{n}{2}\sqrt{3}$),进而得出点A2017的坐标.
解答 解:∵等边三角形△OAB1的一边OA在x轴上,且OA=1,
∴等边三角形的高为$\frac{\sqrt{3}}{2}$,
∵A1B1∥x轴,A1B1=OA=1,
∴A1($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$),
同理可得,A2($\frac{4}{2}$,$\frac{2\sqrt{3}}{2}$),
A3($\frac{5}{2}$,$\frac{3\sqrt{3}}{2}$),
…
由此可得,An($\frac{n+2}{2}$,$\frac{n}{2}\sqrt{3}$),
∴A2017的坐标是($\frac{2019}{2}$,$\frac{2017\sqrt{3}}{2}$),
故答案为:($\frac{2019}{2}$,$\frac{2017\sqrt{3}}{2}$).
点评 本题主要考查了点的坐标变化规律问题,解决问题的关键是依据题意得到点An($\frac{n+2}{2}$,$\frac{n}{2}\sqrt{3}$),解题时注意等边三角形的各边长相等.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
 如图,AB<AC,AD为△ABC的角平分线,E在AC上,AE=AB,BF∥DE交AD于F,求证:四边形BDEF为菱形.
如图,AB<AC,AD为△ABC的角平分线,E在AC上,AE=AB,BF∥DE交AD于F,求证:四边形BDEF为菱形. 已知:△ABC,AB=4,AC=3,以CB为边作等边三角形△CBP,连接AP,求AP的值.
已知:△ABC,AB=4,AC=3,以CB为边作等边三角形△CBP,连接AP,求AP的值.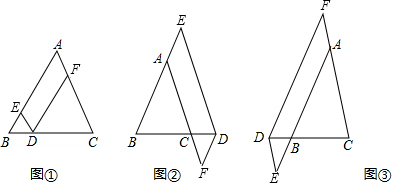
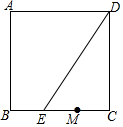 如图,在正方形ABCD中,AB=6,点E、M是边BC的三等分点,连结DE,将△DEC以点M为旋转中心顺时针旋转,当点D的对应点D‘恰好落在正方形的一条边上时,AD‘的长为2或$6-2\sqrt{6}$.
如图,在正方形ABCD中,AB=6,点E、M是边BC的三等分点,连结DE,将△DEC以点M为旋转中心顺时针旋转,当点D的对应点D‘恰好落在正方形的一条边上时,AD‘的长为2或$6-2\sqrt{6}$.