题目内容
AOCD是放置在平面直角坐标系内的梯形,其中0是坐标原点,点A,C,D的坐标分别为(0,8),(5,0),(3,8).若点P在梯形内,且APAD的面积等于APOC的面积,△PAO的面积等于△PCD的面积.
(I)求点P的坐标;
(Ⅱ)试比较∠PAD和∠POC的大小,并说明理由.
(I)求点P的坐标;
(Ⅱ)试比较∠PAD和∠POC的大小,并说明理由.
考点:四边形综合题
专题:
分析:(1)过点P作PE⊥y轴,垂足为E,利用面积相等分别计算PE和OE的长度即可求出P点的坐标;
(2)在AO上取点O′(0,6),利用三角形的外角大于不相邻的外角,结合直角可以比较∠PAD和∠POC的大小.
(2)在AO上取点O′(0,6),利用三角形的外角大于不相邻的外角,结合直角可以比较∠PAD和∠POC的大小.
解答: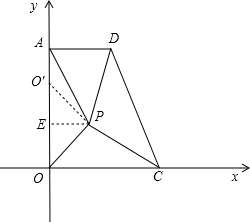 解:(1)如图,过点P作PE⊥y轴于点E,
解:(1)如图,过点P作PE⊥y轴于点E,
∵S△PAD=S△POC,
∴3AE=5OE,即3(8-OE)=5OE,解得OE=3,
∴S△PAD=S△POC=7.5,
S△PAO=S△PCD=
×[
×(3+5)×8-2×7.5]=8.5,
则
×8PE=8.5,即PE=
,
故点P的坐标是(
,3);
(2)∠POC<∠PAD,理由如下:
取O′(0,6),连接PO′,则∠POE=∠PO′E>∠PAE,
从而90°-∠POE<90°-∠PAE,
故∠POC<∠PAD.
 解:(1)如图,过点P作PE⊥y轴于点E,
解:(1)如图,过点P作PE⊥y轴于点E,∵S△PAD=S△POC,
∴3AE=5OE,即3(8-OE)=5OE,解得OE=3,
∴S△PAD=S△POC=7.5,
S△PAO=S△PCD=
| 1 |
| 2 |
| 1 |
| 2 |
则
| 1 |
| 2 |
| 17 |
| 8 |
故点P的坐标是(
| 17 |
| 8 |
(2)∠POC<∠PAD,理由如下:
取O′(0,6),连接PO′,则∠POE=∠PO′E>∠PAE,
从而90°-∠POE<90°-∠PAE,
故∠POC<∠PAD.
点评:本题主要考查三角形的面积及三角形外角的综合应用,掌握求坐标的方法是解题的关键,求点的坐标转化为求线段的长度即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
方程x2-2x-1=0的两个解为x1和x2,则x1+x2的值为( )
| A、2 | B、-2 | C、1 | D、-1 |
 如图,点E在正方形ABCD的边BC的延长线上,且BE=BD,则∠E的度数为( )
如图,点E在正方形ABCD的边BC的延长线上,且BE=BD,则∠E的度数为( )| A、45° | B、60° |
| C、67.5° | D、75° |
 如图,AD∥BC,∠D=90°,DC=7,AD=2,BC=4.若在边DC上有点P使△PAD和△PBC相似,则DP=
如图,AD∥BC,∠D=90°,DC=7,AD=2,BC=4.若在边DC上有点P使△PAD和△PBC相似,则DP=