题目内容
6．解方程组$\left\{\begin{array}{l}{3x+5y=13}\\{4x+3y=10}\end{array}\right.$．分析 根据加减消元法解方程组，首先把x的系数化为相同，然后求出y的值，进而求出x的值．
解答 解：∵$\left\{\begin{array}{l}{3x+5y=13①}\\{4x+3y=10②}\end{array}\right.$，
∴$\left\{\begin{array}{l}{12x+20y=13×4①}\\{12x+9y=10×3②}\end{array}\right.$，
∴①-②：11y=22，
∴y=2，
∴把y=2代入①中得3x+10=13，
∴x=1，
∴$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$．
点评 本题主要考查了解二元一次方程组的知识，解题的关键是掌握加减消元法解方程组，此题基础题．
练习册系列答案
相关题目
如图，直线l1∥l2∥l3，直线AC分别交l1、l2、l3于A、B、C，直线DF分别交l1、l2、l3于D、E、F，AC交DF于H，若AH=2，HB=1，BC=5，则$\frac{DE}{EF}$的值为$\frac{3}{5}$，$\frac{DH}{HF}$的值为$\frac{1}{3}$．
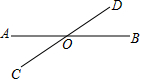如图，已知点O在直线AB上，且∠AOD=∠BOC，则∠AOC与∠AOD互为补角，请说明理由．
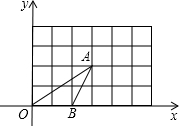如图，△OAB的顶点坐标分别为O（0，0）、A（3，2）、B（2，0），将这三个顶点的坐标同时扩大到原来的2倍，得到对应点D、E、F．
正方形ABCD的边长为6cm，三角形CEF的面积比三角形ABF的面积大6cm2，求出三角形ADE的面积．
如图，在四边形ABCD中，AB=BC，∠ABC=∠CDA=90°，BE⊥AD，垂足为点E．若四边形ABCD的面积为16，则BE=4．