题目内容
已知，∠ABC=30°，O为射线BC上一点，且OB=6，若以O为圆心、4为半径作⊙O，则直线AB与⊙O的位置关系是
- A.相切
- B.相交
- C.相离
- D.无法确定
B
分析：作OD⊥AB于D，根据30°所对的直角边是斜边的一半得：OD=
OB=3＜4，则直线和圆相交．若d＜r，则直线与圆相交；若d=r，则直线于圆相切；若d＞r，则直线与圆相离．
解答：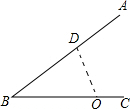
解：作OD⊥AB于D，则OD=OB=3＜4，所以直线和圆相交．
故选B．
点评：此题要根据直角三角形的性质正确计算圆心到直线的距离，然后再由数量关系判断出直线和圆的位置关系．
分析：作OD⊥AB于D，根据30°所对的直角边是斜边的一半得：OD=
OB=3＜4，则直线和圆相交．若d＜r，则直线与圆相交；若d=r，则直线于圆相切；若d＞r，则直线与圆相离．解答：
解：作OD⊥AB于D，则OD=OB=3＜4，所以直线和圆相交．故选B．
点评：此题要根据直角三角形的性质正确计算圆心到直线的距离，然后再由数量关系判断出直线和圆的位置关系．
练习册系列答案
名校课堂系列答案
相关题目
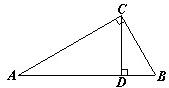20、如图，已知Rt△ABC中，CD⊥AB，∠A=30°，BD=2cm，则AB=
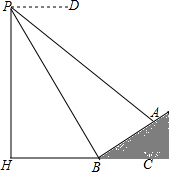（2013•赤峰）如图，数学实习小组在高300米的山腰（即PH=300米）P处进行测量，测得对面山坡上A处的俯角为30°，对面山脚B处的俯角60°．已知tan∠ABC=
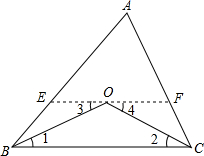如图，已知：∠ABC=50°，∠ACB=60°，BO、CO分别是∠ABC和∠ACB的平分线．求∠BOC．