题目内容
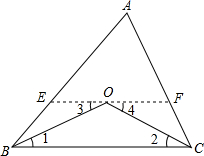 如图,已知:∠ABC=50°,∠ACB=60°,BO、CO分别是∠ABC和∠ACB的平分线.求∠BOC.
如图,已知:∠ABC=50°,∠ACB=60°,BO、CO分别是∠ABC和∠ACB的平分线.求∠BOC.解:过点0作EF∥BC,交AB于点E,交AC于点F.
因为BO平分∠ABC
已知
已知
所以∠1=
| 1 | 2 |
角平分线的定义
角平分线的定义
因为∠ABC=50°
已知
已知
所以∠1=25°
等量代换
等量代换
同理∠2=30°
因为EF∥BC(由作图可知)
所以∠1=∠3
两直线平行,内错角相等
两直线平行,内错角相等
所以∠3=25°
等量代换
等量代换
同理∠4=30°
所以∠BOC=180°-25°-30°=125°.
分析:首先由已知与角平分线的定义,可求得∠1的度数,又由两直线平行,内错角相等,∠3的度数,同理求得∠4的度数,继而求得答案.
解答:解:过点0作EF∥BC,交AB于点E,交AC于点F.
∵BO平分∠ABC,(已知)
∴∠1=
∠ABC,(角平分线的定义)
∵∠ABC=50°,(已知)
∴∠1=25°,(等量代换)
同理∠2=30°,
∵EF∥BC(由作图可知)
∴∠1=∠3,(两直线平行,内错角相等)
∴∠3=25°,(等量代换)
同理∠4=30°
∴∠BOC=180°-25°-30°=125°.
故答案为:已知;角平分线的定义;已知;等量代换;两直线平行,内错角相等;等量代换.
∵BO平分∠ABC,(已知)
∴∠1=
| 1 |
| 2 |
∵∠ABC=50°,(已知)
∴∠1=25°,(等量代换)
同理∠2=30°,
∵EF∥BC(由作图可知)
∴∠1=∠3,(两直线平行,内错角相等)
∴∠3=25°,(等量代换)
同理∠4=30°
∴∠BOC=180°-25°-30°=125°.
故答案为:已知;角平分线的定义;已知;等量代换;两直线平行,内错角相等;等量代换.
点评:此题考查了平行线的性质与角平分线的定义.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
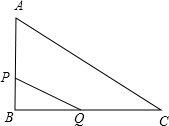
 如图,已知:△ABC中,∠1=∠2,且AE=AD,BE和CD相交于F.求证:BF=CF.
如图,已知:△ABC中,∠1=∠2,且AE=AD,BE和CD相交于F.求证:BF=CF. 如图,已知:△ABC为等边三角形,D、F分别为射线BC、射线AB边上的点,BD=AF,以AD为边作等边△ADE.
如图,已知:△ABC为等边三角形,D、F分别为射线BC、射线AB边上的点,BD=AF,以AD为边作等边△ADE. 如图,已知在△ABC中,AB=AC,∠A=36°,BD为∠ABC的平分线,则
如图,已知在△ABC中,AB=AC,∠A=36°,BD为∠ABC的平分线,则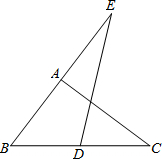 如图,已知在△ABC中,D是边BC的中点,点E在边BA的延长线上,AE=AB,
如图,已知在△ABC中,D是边BC的中点,点E在边BA的延长线上,AE=AB,