Question

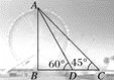
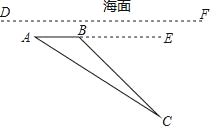
【题目】如图，一艘潜水器在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子(即∠EAC＝30°)，继续在同一深度直线航行1400米到B点处测得正前方C点处的俯角为45°(即∠EBC＝45°)．求海底C点处距离海面DF的深度．(结果保留根号)．

Answer 1

【答案】海底C点处距离海面DF的深度为(700+1300)m．

【解析】

作CM⊥DF于M，交AB于N点，如图，设CN＝x，在Rt△BCE中利用正切定义得到BN＝CN＝x，在Rt△ACN中，利用∠A的正切可求得x的值，然后计算CN+MN即可．

作CM⊥DF于M，交AB于N点，如图，

则MN＝600，AB＝1400，∠NAC＝30°，∠NBC＝45°，

设CN＝x，

在Rt△BCE中，∵tan∠NBC＝tan45°＝，

∴BN＝CN＝x，

在Rt△ACN中，tan∠NAC＝，

∴＝tan30°＝，解得x＝700+700，

∴CM＝CN+MN＝700+700+600＝700+1300，

答：海底C点处距离海面DF的深度为(700+1300)m．