Question

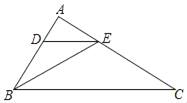
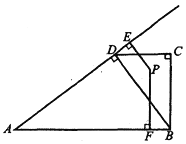
【题目】如图，在四边形中，，，，.点在的边上或内部运动，过点分别向边、所在直线作垂线，交射线于点，交边于点.

（1）求边的长.

（2）求线段的取值范围.

（3）当点在的边上运动时，若，直接写出线段的长.

Answer 1

【答案】（1）.（2）.（或）.（3）线段的长为或.

【解析】

（1）根据tanA=，AB=5可得BD=3，AD=4，由平行线的性质可得∠CDB=∠ABD，根据余弦的定义列出比例式即可求出CD的长；（2）根据点在边上运动时，如图①，取得最小值，点与点重合时，如图②，取得最大值，分别求出AE的值即可；（3）作∠A的平分线，交BD于P1，交BC于P2，则P1E=P1F（D、E重合），P2E=P2F（F、B重合），根据∠FBP1的正切值可求出P1F的值，根据平行线分线段成比例的性质可求出P2F的值即可得答案.

（1）∵，，，

∴，.

∵，

∴.

∴.

∴，即.

∴.

（2）当点在边上运动时，如图1，取得最小值，

此时.

当点与点重合时，如图2，取得最大值.

∵，

∴.

∴.

∴，即.

∴.

∴.

∴.（或）

（3）如图3，作∠A的平分线，交BD于P1，交BC于P2，则P1E=P1F（D、E重合），P2E=P2F（F、B重合），

∵AB=5，AD=4，AD=AF，

∴BF=1，

∵tan∠FBP1===

∴P1F=P1D=，

∵P1F//P2F

∴=，即

∴P2E=P2B=.

∴线段的长为或.