题目内容
已知关于x的方程kx=7-x有正整数解,则整数k的值为 .
考点:一元一次方程的解
专题:
分析:移项合并可得(k+1)x=7,由此可判断出k所能取得的整数值.
解答:解:将原方程变形得kx+x=7即(k+1)x=7,
∵关于x的方程kx=7-x的解为正整数,
∴k+1也为正整数且与x的乘积为7,
可得到k+1=7k+1=1,
解得k=6或k=0.
故k可以取得的整数解为0或6.
故答案是:0或6.
∵关于x的方程kx=7-x的解为正整数,
∴k+1也为正整数且与x的乘积为7,
可得到k+1=7k+1=1,
解得k=6或k=0.
故k可以取得的整数解为0或6.
故答案是:0或6.
点评:本题考查解一元一次方程的知识,注意理解方程的解为整数所表示的含义.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知M(a,3)和N(4,b)关于y轴对称,则(a+b)2014的值为( )
| A、1 |
| B、-1 |
| C、72014 |
| D、-72014 |
 如图,a∥b,点P在直线a上,点A在直线b上,PA⊥b,PA=5cm,则点A到直线a的距离为
如图,a∥b,点P在直线a上,点A在直线b上,PA⊥b,PA=5cm,则点A到直线a的距离为 从正面、左面、上面观察如图所示的几何体,分别画出你所看到的几何体的形状图.
从正面、左面、上面观察如图所示的几何体,分别画出你所看到的几何体的形状图. 如图,直线l是一次函数y=kx+b的图象,若点A(x1,y1)和B(x2,y2)在直线l上,且x1<x2,则y1与y2的大小关系是
如图,直线l是一次函数y=kx+b的图象,若点A(x1,y1)和B(x2,y2)在直线l上,且x1<x2,则y1与y2的大小关系是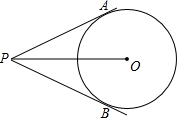 已知PA切⊙O于点A,PB切⊙O于点B,PO=4,PA=2
已知PA切⊙O于点A,PB切⊙O于点B,PO=4,PA=2