题目内容
如图,△ABC的内切圆分别切BC、CA、AB于点D、E、F,过点F作BC的平行线分别交直线DA、DE于点H、G.问:图中除由切线长定理可知AF=AE,BF=BD,CD=CE外,还有相等的线段吗?若有,请指出来,并加以证明.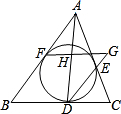


有相等的线段:HG=HF
过点A作FG的平行线分别交DF、DG的延长线于点M、N
则∠AMF=∠BDF
由切线长定理知BF=BD、AF=AE.
所以∠BDF=∠BFD,
又∵∠BFD=∠AFM,
∴∠AMF=∠AFM,
∴AM=AF,
同理:AN=AE,
∴AM=AN,
又FG∥MN,
∴△DFH∽△DMA,
| HF |
| AM |
| DH |
| DA |
同理:
| HG |
| AN |
| DH |
| DA |
∴
| HF |
| AM |
| HG |
| AN |
∴HG=HF.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
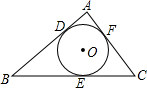 已知如图,△ABC内切⊙O于D、E、F三点,内切圆⊙O的半径为1,∠C=60°,AB=5,则△ABC的周长为( )
已知如图,△ABC内切⊙O于D、E、F三点,内切圆⊙O的半径为1,∠C=60°,AB=5,则△ABC的周长为( )| A、12 | ||
| B、14 | ||
C、10+2
| ||
D、10+
|
 5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.
5、已知:如图,△ABC内接于⊙O,AE切⊙O于点A,BD∥AE交AC的延长线于点D,求证:AB2=AC•AD.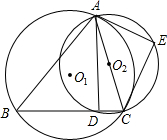 点E,连接AD、CE,若AC=7,AD=3
点E,连接AD、CE,若AC=7,AD=3
