题目内容
如图ABCD是边长为a的正方形，以D为圆心，DA为半径的圆弧与以BC为直径的半圆交于另一点P，延长AP交BC于点N，则| BN |
| NC |
考点：相似三角形的判定与性质,勾股定理,正方形的性质,圆周角定理
专题：计算题
分析：设点S为BC的中点，连接，DP，DS，DS与PC交于点W，作PE⊥BC于点E，PF⊥AB于点F，从而可证△DCS≌△DPS，也推∠DPS=∠DCB=90°，然后求出PC，再根据勾股定理求出PB，利用三角形的面积，求得PE，利用勾股定理求得PF，利用相似求得BN的长，即可解答出．
解答：
解：如图，设点S为BC的中点，连接DP，DS，DS与PC交于点W，作PE⊥BC于点E，PF⊥AB于点F，
∴DP=CD=a，PS=CS=
a，即DS是PC的中垂线，
∴△DCS≌△DPS，
∴∠DPS=∠DCB=90°，
∴DS=
=
=
a，
由三角形的面积公式可得PC=
a，
∵BC为直径，
∴∠CPB=90°，
∴PB=
=
a，
∴PE=FB=
=
a，
∴PF=BE=
=
a，
∴AF=AB-FB=
a，
∴
=
，即
=
，
∴BN=
a，
∴NC=
a，
∴
=
；
故答案为：
．
解：如图，设点S为BC的中点，连接DP，DS，DS与PC交于点W，作PE⊥BC于点E，PF⊥AB于点F，∴DP=CD=a，PS=CS=
| 1 |
| 2 |
∴△DCS≌△DPS，
∴∠DPS=∠DCB=90°，
∴DS=
| DC2+CS2 |
a2+
|
| ||
| 2 |
由三角形的面积公式可得PC=
2
| ||
| 5 |
∵BC为直径，
∴∠CPB=90°，
∴PB=
| BC2-PC2 |
| ||
| 5 |
∴PE=FB=
| PC•PB |
| BC |
| 2 |
| 5 |
∴PF=BE=
| PB2-PE2 |
| 1 |
| 5 |
∴AF=AB-FB=
| 3 |
| 5 |
∴
| AF |
| AB |
| PF |
| BN |
| ||
| a |
| ||
| BN |
∴BN=
| 1 |
| 3 |
∴NC=
| 2 |
| 3 |
∴
| BN |
| NC |
| 1 |
| 2 |
故答案为：
| 1 |
| 2 |
点评：本题主要考查了正方形的性质，中垂线的性质，勾股定理，相似三角形的判定，作好辅助线，是解答本题的关键．
练习册系列答案
王后雄学案教材完全解读系列答案
相关题目
设n=120120120120，则n2（用10进制表示）的各位数字和是（ ）
| A、60 | B、81 | C、90 | D、99 |
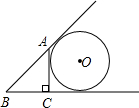如图AC⊥BC于C，BC=a，CA=b，AB=c，⊙O与直线AB、BC、AC都相切，则⊙O的半径为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
从有关方面获悉，在我市农村己经实行了农民新型合作医疗保险制度．享受医保的农民可在规定的医院就医并按规定标准报销部分医疗费用．下表是医疗费用报销的标准：
若某农民一年内本人自负住院医疗费17000元（自负医疗费=实际医疗费-按标准报销的金额），则该农民当年实际医疗费用共（ ）元．
| 医疗费用范围 | 门诊 | 住院 | ||
| 0-5000元 | 5001-20000元 | 20000元以上 | ||
| 每年报销比例标准 | 30% | 30% | 40% | 50% |
| A、29000 | B、27500 |
| C、6300 | D、32000 |
方程
=0.2可变形为（ ）
| x-0.1 |
| 0.3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|