��Ŀ����
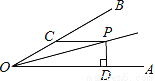
��֪����ͼ����ֱ��������ABC�У���ACB=900��D��AB��һ�㣬�ҡ�ACD=��B
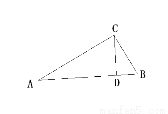
��1���жϡ�ACD����״����˵�����ɡ�
��2������֤����Ľ��۹�����Ӧ������һ�Ի���������⣿
�𣺡�ACD��ֱ�������� ���ɣ���֤��ACD�ס�ABC ����Ӧ�ǡ�ACD=��ACB=90������CD��AB ����������⣺�������������ƣ���Ӧ����ȡ� ����ֱ�������ζ�Ӧ����ȣ����������������ơ� �������� ���������������֪��ACD=��B���ҡ�A =��A���ɵá�ACD�ס�ABC����Ϊ��ACB=900 ���Զ�Ӧ�ǡ�ACD=��ACB=90�㡣���ACD��ֱ�������� ...
��ϰ��ϵ�д�
�����Ŀ



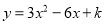 ��
��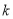 Ϊ������ͼ����
Ϊ������ͼ����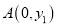 ��
�� 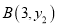 ��
�� 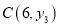 ������( )
������( )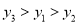 B.
B. 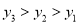 C.
C. 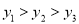 D.
D. 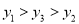
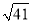 C. 3��
C. 3��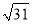 D. 3��
D. 3��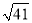
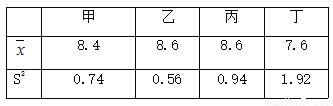
 ���䷽��S2���±���ʾ��
���䷽��S2���±���ʾ��