题目内容
11．现有一块半径为$\sqrt{2}$R的圆形铁皮，用它裁一块面积最大的正方形铁皮的边长是2R．分析 因为要想裁出一块面积最大的正方形，需要正方形边长最长，所以正方形的四个顶点在圆周上，由此可画出图形；连接OA，DO，在Rt△AOD中，由勾股定理可得出边长．
解答 
解：要想裁出一块面积最大的正方形，需要正方形边长最长，所以正方形的四个顶点在圆周上，
如图所示：
连接OA，DO，则：OA=OD=$\sqrt{2}$R，
在Rt△AOD中，由勾股定理得：
AD2=（$\sqrt{2}$R）2+（$\sqrt{2}$R）2，
则AD=2R，
故该正方形的边长为2R，
故答案为：2R．
点评 本题考查了勾股定理和正方形的性质以及二次根式的应用，正确利用勾股定理得出是解题关键．
练习册系列答案
相关题目
1．
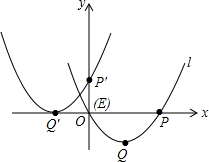如图，将抛物线l：y=ax2-2x+a2-4（a为常数）向左并向上平移，使顶点Q的对应点Q′，抛物线l与x轴的右交点P的对应点P′分别在两坐标轴上，则抛物线l与x轴的交点E的对应点的坐标为（ ）
如图，将抛物线l：y=ax2-2x+a2-4（a为常数）向左并向上平移，使顶点Q的对应点Q′，抛物线l与x轴的右交点P的对应点P′分别在两坐标轴上，则抛物线l与x轴的交点E的对应点的坐标为（ ）| A． | （-1，$\frac{1}{2}$） | B． | （0，0） | C． | （-$\frac{1}{2}$，1） | D． | （-$\frac{1}{2}$，0） |
如图，在△ABC中，∠ACB=80°，∠ABC=60°．按以下步骤作图：①以点A为圆心，小于AC的长为半径画弧，分别交AB、AC于点E、F；②分别以点E、F为圆心，大于$\frac{1}{2}$EF的长为半径画弧，两弧相交于点G；③作射线AG交BC于点D．则∠ADB的度数为100°．
如图，将一长方形纸条ABCD沿AE折叠，使点B落在点B′处，已知∠ABD=70°，那么当∠BAE为多少时，才能使AB′∥BD？