题目内容
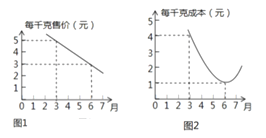
【题目】某种蔬菜每千克售价![]() (元)与销售月份
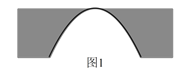
(元)与销售月份![]() 之间的关系如图1所示,每千克成本
之间的关系如图1所示,每千克成本![]() (元)与销售月份
(元)与销售月份![]() 之间的关系如图2所示,其中图1中的点在同一条线段上,图2中的点在同一条抛物线上,且抛物线的最低点的坐标为(6,1).
之间的关系如图2所示,其中图1中的点在同一条线段上,图2中的点在同一条抛物线上,且抛物线的最低点的坐标为(6,1).
(1)求出![]() 与
与![]() 之间满足的函数表达式,并直接写出
之间满足的函数表达式,并直接写出![]() 的取值范围;
的取值范围;
(2)求出![]() 与
与![]() 之间满足的函数表达式;
之间满足的函数表达式;
(3)设这种蔬菜每千克收益为![]() 元,试问在哪个月份出售这种蔬菜,
元,试问在哪个月份出售这种蔬菜,![]() 将取得最大值?并求出此最大值.(收益=售价-成本)
将取得最大值?并求出此最大值.(收益=售价-成本)
【答案】(1)y1=﹣![]() x+7(3≤x≤6);(2)y2=
x+7(3≤x≤6);(2)y2=![]() (x﹣6)2+1;(3)5月出售这种蔬菜,每千克收益最大
(x﹣6)2+1;(3)5月出售这种蔬菜,每千克收益最大
【解析】
(1)设y1=kx+b,y2=a(x-b)2+c,代入各点求出未知量,(2)收益=售价-成本,列出函数解析式,求出最大值.
(1)设y1=kx+b,
∵直线经过(3,5)、(6,3),
![]() ,解得:
,解得: ,
,
∴y1=﹣![]() x+7(3≤x≤6),
x+7(3≤x≤6),
(2)设y2=a(x﹣6)2+1,
把(3,4)代入得:4=a(3﹣6)2+1,
解得a=![]() ,
,
∴y2=![]() (x﹣6)2+1,
(x﹣6)2+1,
(3)由题意得:w=y1﹣y2=﹣![]() x+7﹣[
x+7﹣[![]() (x﹣6)2+1],
(x﹣6)2+1],
=﹣![]() x2+
x2+![]() =﹣
=﹣![]() ,
,
当x=5时,y最大值=![]() .
.
故5月出售这种蔬菜,每千克收益最大.

练习册系列答案
相关题目
【题目】随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了![]() 两种上网学习的月收费方式.
两种上网学习的月收费方式.
收费方式 | 月使用费/元 | 包时上网时间/ | 超时费/(元/ |
| 12 | 40 | 0.5 |
|
|
| 0.6 |
设每月上网学习时间为![]() 小时,方案
小时,方案![]() 的收费金额分别为
的收费金额分别为![]() ,
,![]() .
.
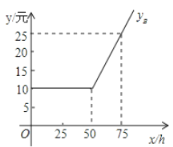
(1)如图是![]() 与
与![]() 之间的函数关系图象,请根据图象填空:
之间的函数关系图象,请根据图象填空:![]() = ;
= ;![]() =
=
(2)求出![]() 与
与![]() (
(![]() )之间的函数关系式.
)之间的函数关系式.
(3)如果每月上网时间为60小时,选择哪种方式网上学习合算,为什么?