Question

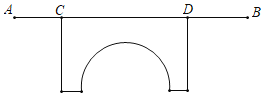
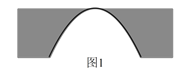
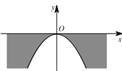
【题目】河上有一座桥孔为抛物线形的拱桥（如图 ），水面宽 时，水面离桥孔顶部 ，因降暴雨水面上升 ．

（1）建立适当的坐标系，并求暴雨后水面的宽；（结果保留根号）

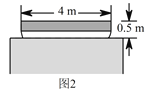
（2）一艘装满物资的小船，露出水面的部分高为 ，宽 （横断面如图 所示），暴雨后这艘船能从这座拱桥下通过吗?

Answer 1

【答案】（1）水面宽为 米；（2）这艘船能从这座拱桥下通过．

【解析】试题分析：

（1）建立如下图所示的平面直角坐标系，由题意设抛物线型拱桥的解析式为：y=ax2，由题意可知此抛物线过点（3，-3），由此即可求出抛物线的解析式，把y=-2代入所得解析式，解此对应的x的值，即可求得此时水面的宽；

（2）由题意在（1）中所得的解析式中，求出当x=2时对应的y的值，比较此时y的值的绝对值和1.5的大小即可得出结论.

试题解析：

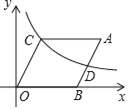
（1） 如图，以抛物线的顶点为原点，以桥面为 轴，建立平面直角坐标系，由题意可知抛物线过点 ，

设抛物线的函数表达式为： ．

把 代入 ，可求 ，

则抛物线对应的函数表达式为 ．

当水面上涨 米后，水面所在的位置为直线 ，

令 得，则，解得： ， ，

∴此时水面宽为为： （米）；

（2）由题意 ：当船在桥拱的正中心航行时，船的边缘距抛物线对称轴水平距离为 米，在中，令 得， ，

∵船上货物最高点距拱顶为： （米）且 ，

∴这艘船能从这座拱桥下通过．