题目内容
9.如图1是一种包装盒的表面展开图,将它围起来可得到一个几何体的模型.(1)这个几何体模型的名称是长方体或底面为长方形的直棱柱.
(2)如图2是根据a,b,h的取值画出的几何体的主视图和俯视图(图中实线表示的长方形),请在网格中画出该几何体的左视图.
(3)若h=a+b,且a,b满足$\frac{1}{4}$a2+b2-a-6b+10=0,求该几何体的表面积.
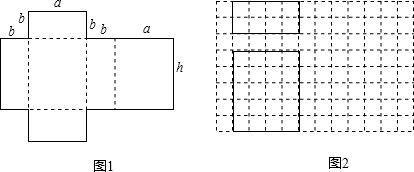
分析 (1)侧面四个长方形和上下两个底面也是长方形,所以折叠后能围成长方体.
(2)根据图1所标注的相关线段的长度画出其左视图;
(3)对$\frac{1}{4}$a2+b2-a-6b+10=0进行因式分解,求得a、b的值,则易求h的值,然后由几何体的表面积计算公式进行解答.
解答 解:(1)根据该包装盒的表面展开图知,该几何体模型的名称为:长方体或底面为长方形的直棱柱.
故答案是:长方体或底面为长方形的直棱柱;
(2)如图所示: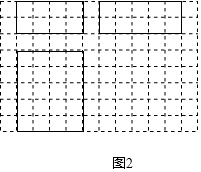
(3)由题意得,($\frac{1}{2}$a-1)2+(b-3)2=0,
则a=2,b=3,
所以h=a+b=2+3=5.
所以表面积为:2(2×3+5×2+3×5)=62.
点评 本题考查了因式分解的应用,由三视图判断几何体等知识点.几何体的三视图画法.由几何体的俯视图及小正方形内的数字,可知主视图的列数与俯视数的列数相同,且每列小正方形数目为俯视图中该列小正方形数字中的最大数字.左视图的列数与俯视图的行数相同,且每列小正方形数目为俯视图中相应行中正方形数字中的最大数字.

练习册系列答案
相关题目
19.据国家统计局发布的数据显示,2015年一季度我国国内生产总值约为14060000000000元,这个数字用科学记数法表示为( )
| A. | 1.406×1013 | B. | 14.06×1012 | C. | 1.406×1012 | D. | 140.6×1011 |
20.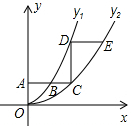 如图,平行于x轴的直线AC分别交抛物线y1=x2(x≥0)与y2=$\frac{{x}^{2}}{4}$(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则$\frac{DE}{AB}$=( )
如图,平行于x轴的直线AC分别交抛物线y1=x2(x≥0)与y2=$\frac{{x}^{2}}{4}$(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则$\frac{DE}{AB}$=( )
 如图,平行于x轴的直线AC分别交抛物线y1=x2(x≥0)与y2=$\frac{{x}^{2}}{4}$(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则$\frac{DE}{AB}$=( )
如图,平行于x轴的直线AC分别交抛物线y1=x2(x≥0)与y2=$\frac{{x}^{2}}{4}$(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则$\frac{DE}{AB}$=( )| A. | 2:1 | B. | $\sqrt{2}$:1 | C. | $\sqrt{5}$:1 | D. | 3:1 |
17.已知抛物线y=ax2+bx+c(a≠0)经过点(1,1)和(-1,0).下列结论:
①b2>4ac;
②抛物线的对称轴为x=-$\frac{1}{4a}$;
③a-b+c=0;
④当a<0时,抛物线与x轴必有一个交点在点(1,0)的右侧.
其中结论正确的个数有( )
①b2>4ac;
②抛物线的对称轴为x=-$\frac{1}{4a}$;
③a-b+c=0;
④当a<0时,抛物线与x轴必有一个交点在点(1,0)的右侧.
其中结论正确的个数有( )
| A. | 4个 | B. | 1个 | C. | 2个 | D. | 3个 |
18.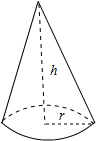 如图,圆锥体的高h=2$\sqrt{3}$cm,底面圆半径r=2cm,则圆锥体的全面积为( )
如图,圆锥体的高h=2$\sqrt{3}$cm,底面圆半径r=2cm,则圆锥体的全面积为( )
 如图,圆锥体的高h=2$\sqrt{3}$cm,底面圆半径r=2cm,则圆锥体的全面积为( )
如图,圆锥体的高h=2$\sqrt{3}$cm,底面圆半径r=2cm,则圆锥体的全面积为( )| A. | 4$\sqrt{3}$πcm2 | B. | 8πcm2 | C. | 12πcm2 | D. | (4$\sqrt{3}$+4)πcm2 |
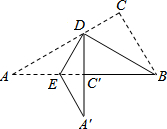 如图,在Rt△ABC中,∠ACB=90°,将△ABC沿BD折叠,点C恰巧落在边AB上的C′处,折痕为BD,再将其沿DE折叠,使点A落在DC′的延长线上的A′处.若△BED与△ABC相似,则相似比$\frac{BD}{AC}$=$\frac{2}{3}$.
如图,在Rt△ABC中,∠ACB=90°,将△ABC沿BD折叠,点C恰巧落在边AB上的C′处,折痕为BD,再将其沿DE折叠,使点A落在DC′的延长线上的A′处.若△BED与△ABC相似,则相似比$\frac{BD}{AC}$=$\frac{2}{3}$.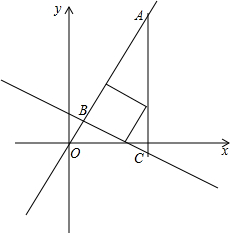 如图,在平面直角坐标系中,直线y=-$\frac{1}{2}$x+$\frac{5}{2}$交直线y=kx(k>0)于点B,平行于y轴的直线x=7交它们于点A、C,且AC=15.
如图,在平面直角坐标系中,直线y=-$\frac{1}{2}$x+$\frac{5}{2}$交直线y=kx(k>0)于点B,平行于y轴的直线x=7交它们于点A、C,且AC=15.